题目内容
用数学归纳法证明:f(n)=(2n+7)·3n+9(n∈N*)能被36整除.
证明:① 当n=1时,f(1)=(2×1+7)×3+9=36,能被36整除.
② 假设n=k时,f(k)能被36整除,则当n=k+1时,f(k+1)=[2(k+1)+7]·3k+1+9=3[(2k+7)·3k+9]+18(3k-1-1),由归纳假设3[(2k+7)·3k+9]能被36整除,而3k-1-1是偶数,所以18(3k-1-1)能被36整除.所以n=k+1时,f(n)能被36整除.
由①②知,对任何n∈N,f(n)能被36整除.

练习册系列答案
相关题目
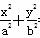 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=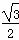 ,连结椭圆的四个顶点得到的菱形的面积为4.
,连结椭圆的四个顶点得到的菱形的面积为4.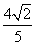 ,求直线l的倾斜角.
,求直线l的倾斜角. ,如图,在长方体ABCD
,如图,在长方体ABCD A1B1C1D1中,四面体A1
A1B1C1D1中,四面体A1
 ,an+1=
,an+1= ,则a2,a3,a4,a5的值分别为________________,由此猜想an=________.
,则a2,a3,a4,a5的值分别为________________,由此猜想an=________. 集合
集合 ,
, ,下图中阴影部分所表示的集合为
,下图中阴影部分所表示的集合为 B.
B. 
 D.
D. 

 ,
, ,
, ,则
,则  (B)
(B) (C)
(C) (D)
(D) 
 的零点所在的区间是________.
的零点所在的区间是________.