题目内容
20.函数y=$\frac{1}{\sqrt{4-3x-{x}^{2}}}$+(x+1)0的定义域为( )| A. | [-4,1] | B. | (-4,1) | C. | [-4,-1) | D. | (-4,-1)∪(-1,1) |
分析 根据二次根式以及幂函数的定义求出x的范围即可.
解答 解:由题意得:
$\left\{\begin{array}{l}{4-3x{-x}^{2}>0}\\{x+1≠0}\end{array}\right.$,
解得:-4<x<1且x≠-1,
故函数的定义域是(-4,-1)∪(-1,1),
故选:D.
点评 本题考查了求函数的定义域问题,考查二次根式的性质,是一道基础题.

练习册系列答案
相关题目
11.曲线$\left\{\begin{array}{l}x=5cosθ\\ y=4sinθ\end{array}$(θ为参数)的焦点到双曲线x2-$\frac{y^2}{2}$=1的渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
5.直线ax+2y=0平行于直线x+y=1,则a等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
12.下列四个函数中,在定义域上是减函数的是( )
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x3 | C. | f(x)=-x2 | D. | f(x)=-x |
9.已知sinα=$\frac{{2\sqrt{2}}}{3}$,cos(α+β)=-$\frac{1}{3}$,且α,β∈(0,$\frac{π}{2}$),则sin(α-β)的值等于( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{10\sqrt{2}}}{27}$ |
10.直线x=$\frac{π}{3}$的倾斜角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
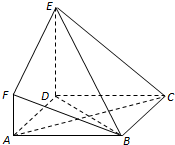 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$. 如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.