题目内容
8．已知动点A（xA，yA）在直线l：y=6-x上，动点B在圆C：x2+y2-2x-2y-2=0上，若∠CAB=30°，则xA的最大值为（ ）| A． | 2 | B． | 4 | C． | 5 | D． | 6 |
分析 由题意，当AB是圆的切线时，∠CAB最大，此时CA=4，即可求得点A的横坐标的最大值．
解答 解：由题意，当AB是圆的切线时，∠CAB最大，此时CA=4，
即可求得点A的横坐标的最大值．
点A的坐标满足：（x-1）2+（y-1）2=16与y=6-x，
解得x=5或x=1．
∴点A的横坐标的最大值为5．
故选C．
点评 本题主要考查直线与圆的位置关系的判断，以及转化与化归的思想方法．正确理解题意是解答该题的关键，是中档题．
练习册系列答案
相关题目
16．已知函数f（x）=sinωx+acosωx（ω＞0）的图象过点$A（0，\sqrt{3}）$，且$f（x+\frac{π}{2}）=-f（x）$，将其图象向右平移m（m＞0）个单位长度，所得函数图象关于y轴对称，则m的最小值为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{12}$ |
3．
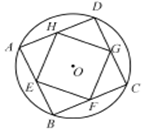如图，ABCD是以O为圆心、半径为2的圆的内接正方形，EFGH是正方形ABCD的内接正方形，且E、F、G、H分别为AB、BC、CD、DA的中点．将一枚针随机掷到圆O内，用M表示事件“针落在正方形ABCD内”，N表示事件“针落在正方形EFGH内”，则P（N|M）=（ ）
如图，ABCD是以O为圆心、半径为2的圆的内接正方形，EFGH是正方形ABCD的内接正方形，且E、F、G、H分别为AB、BC、CD、DA的中点．将一枚针随机掷到圆O内，用M表示事件“针落在正方形ABCD内”，N表示事件“针落在正方形EFGH内”，则P（N|M）=（ ）| A． | $\frac{1}{π}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
13．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a，b＞0）$的离心率为$\sqrt{5}$，则抛物线y2=4x的焦点到双曲线的渐近线的距离是（ ）
| A． | $\frac{{\sqrt{5}}}{10}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{2\sqrt{5}}}{5}$ | D． | $\frac{{4\sqrt{5}}}{5}$ |
20．设i为虚数单位，若复数$\frac{z}{-i}$在复平面内对应的点为（1，2），则z=（ ）
| A． | -2+i | B． | 2-i | C． | -1+2i | D． | 1-2i |
17．设x，y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-1≥0\\ x≤3\end{array}\right.$，则z=2x-3y的最大值是（ ）
| A． | -3 | B． | -6 | C． | 15 | D． | 12 |
18．若集合A={-2，0，1}，B={x|x＜-1或x＞0}，则A∩B=（ ）
| A． | {-2} | B． | {1} | C． | {-2，1} | D． | {-2，0，1} |