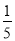题目内容
17.若一个三棱锥中,有一条棱长为a,其余棱长均为1,则其体积F(a)取得最大值时a的值为( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
分析 由题意画出三棱锥的图形,取BC,AD的中点分别为E,F,求出AED的面积,然后求出棱锥的体积.
解答 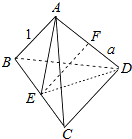 解:由题意画出棱锥的图形,AB=BC=CD=BD=AC=1,AD=a;
解:由题意画出棱锥的图形,AB=BC=CD=BD=AC=1,AD=a;
取BC,AD的中点分别为E,F,
可知平面AED垂直BC,S△AED=$\frac{1}{2}$AD•EF
EF=$\sqrt{{(\frac{\sqrt{3}}{2})}^{2}-{(\frac{x}{2})}^{2}}$
所以F(a)=$\frac{1}{3}$•S△AED•BC=$\frac{1}{12}$a$\sqrt{3-{a}^{2}}$=$\frac{1}{12}$$\sqrt{3{a}^{2}-{a}^{4}}$,
令y=3a2-a4=3t-t2.t=a2.当t=$\frac{3}{2}$,即a=$\frac{\sqrt{6}}{2}$时,体积F(a)取得最大值.
故选:D.
点评 本题是基础题,考查空间想象能力,计算能力,本题的关键是棱锥的转化为两个棱锥,底面AED的处理是解题的关键.

练习册系列答案
相关题目
8.如图是一个空间几何体的三视图,则该几何体的体积是( )


| A. | 4-4π | B. | 8-$\frac{2π}{3}$ | C. | 4-2π | D. | 4-$\frac{2π}{3}$ |
9.一个几何体的三视图如图所示,则这个几何体的外接球的体积为( )
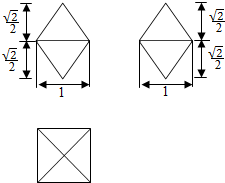

| A. | $\frac{{\sqrt{2}}}{3}π$? | B. | $\sqrt{2}π$? | C. | 2π? | D. | $\frac{{2\sqrt{2}}}{3}π$? |
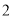 个白球和
个白球和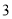 个黑球,则先摸出个白球后放回,再摸出个白球的概率是( )
个黑球,则先摸出个白球后放回,再摸出个白球的概率是( )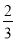 B.
B.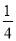 C.
C.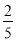 D.
D.