题目内容
2.函数f(x)满足:f(a+b)=f(a)•f(b)且f(1)=2则$\frac{{{f^2}(1)+f(2)}}{f(1)}+\frac{{{f^2}(2)+f(4)}}{f(3)}+\frac{{{f^2}(3)+f(6)}}{f(5)}+…\frac{{{f^2}(1008)+f(2016)}}{f(2015)}$=4032.分析 由已知中f(a+b)=f(a)•f(b),可得:$\frac{{f}^{2}(\frac{a+1}{2})+f(a+1)}{f(a)}$=$\frac{2f(a+1)}{f(a)}$=2f(1)=4,进而得到答案.
解答 解:∵f(a+b)=f(a)•f(b),
∴$\frac{{f}^{2}(\frac{a+1}{2})+f(a+1)}{f(a)}$=$\frac{2f(a+1)}{f(a)}$=2f(1)=4,
∴$\frac{{f}^{2}(1)+f(2)}{f(1)}+\frac{{f}^{2}(2)+f(4)}{f(3)}+\frac{{f}^{2}(3)+f(6)}{f(5)}+…\frac{{f}^{2}(1008)+f(2016)}{f(2015)}$=4×$\frac{2015+1}{2}$=4032,
故答案为:4032
点评 本题考查的知识点是抽象函数及其应用,其中根据已知得到$\frac{{f}^{2}(\frac{a+1}{2})+f(a+1)}{f(a)}$=$\frac{2f(a+1)}{f(a)}$=2f(1)=4,是解答的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
10.${∫}_{0}^{1}$(2x+6x2)dx=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.若一个三棱锥中,有一条棱长为a,其余棱长均为1,则其体积F(a)取得最大值时a的值为( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
7.已知集合M={3,log2a},N={a,b},若M∩N={0},则M∪N=( )
| A. | {0,1,2} | B. | {0,1,3} | C. | {0,2,3} | D. | {1,2,3} |
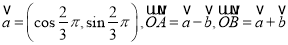 ,若
,若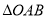 是以
是以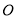 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则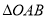 的面积等于( )
的面积等于( ) C.2 D.
C.2 D.