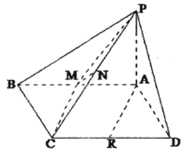
题目内容
【题目】正方形![]() 沿对角线
沿对角线![]() 折成直二面角,下列结论:①异面直线
折成直二面角,下列结论:①异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④二面角
是等边三角形;④二面角![]() 的平面角正切值是
的平面角正切值是![]() ;其中正确结论是______.(写出你认为正确的所有结论的序号)
;其中正确结论是______.(写出你认为正确的所有结论的序号)
【答案】①②③④
【解析】
作出翻折后的空间图形,取![]() 为
为![]() 的中点,根据面面垂直的性质有
的中点,根据面面垂直的性质有![]() 平面
平面![]() ,然后对各个选项进行分析计算,从而判断其真假.
,然后对各个选项进行分析计算,从而判断其真假.
设正方形![]() 的边长为2,取
的边长为2,取![]() 的中点为
的中点为![]() ,连结
,连结![]() .
.
由![]() ,有
,有![]() 。
。
又因为![]() 直二面角,所以
直二面角,所以 ![]() 平面
平面![]() .
.
在直角三角形![]() 中,
中,![]() .则
.则![]() .
.
对①,取![]() 的中点分别为
的中点分别为![]() ,连结
,连结![]() .
.
则![]() ∥
∥![]() 且
且![]() =1,
=1,![]() ∥
∥![]() 且
且![]() =1.
=1.
所以异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
直角三角形![]() 中,
中,![]() ,所以
,所以![]() 为等边三角形.
为等边三角形.
则![]() ,所以①正确.
,所以①正确.
对②,由![]() ,有
,有![]() ,
,
则可以得到![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() 。
。
所以![]()
![]() ,所以②正确.
,所以②正确.
对③,由题意可知![]() ,
,![]() 是等边三角形.
是等边三角形.
所以③正确.
对④,由![]() ∥
∥![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在直角三角形![]() 中,
中,![]() ,所以所以④正确.
,所以所以④正确.
故答案为:①②③④.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目