题目内容
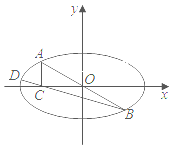
【题目】已知椭圆![]() ,定义椭圆
,定义椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() .
.
(1)求椭圆![]() 上的点
上的点![]() 的“伴随点”
的“伴随点”![]() 的轨迹方程;
的轨迹方程;
(2)如果椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() ,对于椭圆
,对于椭圆![]() 上的任意点
上的任意点![]() 及它的“伴随点”
及它的“伴随点”![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,直线
时,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,若点
两点,若点![]() ,
, ![]() 的“伴随点”分别是
的“伴随点”分别是![]() ,
, ![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)利用相关点代入法求解;(2)先由已知求得椭圆方程为![]() ,设
,设![]()
![]()
![]()
![]() ;(3)设
;(3)设![]() , 1)当直线
, 1)当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为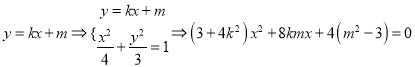
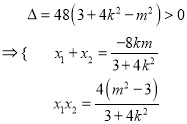 ,由以
,由以![]() 为直径的圆经过原点
为直径的圆经过原点![]()
![]()
![]()
![]() ,又
,又![]() 到直线的距离
到直线的距离![]() ;2) 当直线
;2) 当直线![]() 的斜率不存在时,设方程为
的斜率不存在时,设方程为
![]()
![]() 的面积是定值
的面积是定值![]() .
.
试题解析:(1)解.设![]() (
(![]() )由题意
)由题意 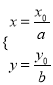 则
则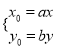 ,又
,又![]()
![]()
![]() ,从而得
,从而得![]()
(2)由![]() ,得
,得![]() .又
.又![]() ,得
,得![]() .
.
![]() 点
点![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]() ,且
,且![]() ,
,
![]()
![]() ,
,
由于![]() ,
, ![]() 的取值范围是
的取值范围是![]()
(3) 设![]() ,则
,则![]() ;
;
1)当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() , 由
, 由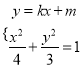
得![]() ; 有
; 有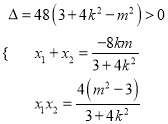 ①
①
由以![]() 为直径的圆经过坐标原点O可得:
为直径的圆经过坐标原点O可得: ![]() ;
;
整理得: ![]() ②
②
将①式代入②式得: ![]() ,
,
![]()
又点![]() 到直线
到直线![]() 的距离
的距离![]()
![]()
所以![]()
2) 当直线![]() 的斜率不存在时,设方程为
的斜率不存在时,设方程为![]()
联立椭圆方程得![]() ;代入
;代入![]() 得
得![]() ,解得
,解得![]() ,从而
,从而![]() ,
,![]() 综上:
综上: ![]() 的面积是定值
的面积是定值![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目