题目内容
方程2x2+x3=2的解的个数为 .
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:构造函数,求出函数的极值,判断极值的符号,即可得到结论.
解答:
解:由程2x2+x3=2得程2x2+x3-2=0,
设f(x)=2x2+x3-2,
则函数的导数f′(x)=3x2+4x=x(3x+4),
由f′(x)>0得x>0或x<-
,此时函数单调递增,
由f′(x)<0得-
<x<0,此时函数单调递减,
则当x=0时,函数取得极小值f(0)=-2<0,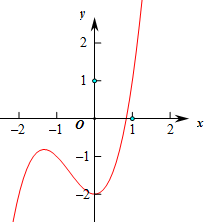
当x=-
,函数取得极大值f(-
)=
-2<0,
则函数f(x)的零点个数为1个,
故方程2x2+x3=2的解的个数为1个,
故答案为:1
设f(x)=2x2+x3-2,
则函数的导数f′(x)=3x2+4x=x(3x+4),
由f′(x)>0得x>0或x<-
| 4 |
| 3 |
由f′(x)<0得-
| 4 |
| 3 |
则当x=0时,函数取得极小值f(0)=-2<0,

当x=-
| 4 |
| 3 |
| 4 |
| 3 |
| 32 |
| 27 |
则函数f(x)的零点个数为1个,
故方程2x2+x3=2的解的个数为1个,
故答案为:1
点评:本题主要考查方程解的个数的判断,根据方程和函数的关系,构造函数,利用函数极值和导数之间的关系,求出函数的极值是解决本题的关键.

练习册系列答案
相关题目
在等差数列{an}中,a1=3,a1+a2+a3=12,则a4+a5+a6=( )
| A、28 | B、27 | C、26 | D、21 |