题目内容
求下列函数的值域:f(x)=-x2-2x+3(-2≤x≤3)； f(x)=2x2-4x+3(2≤x≤3).
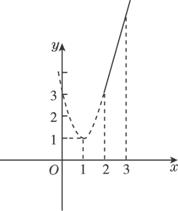
思路解析:求二次函数的值域,要结合图形和函数的定义域,利用数形结合法来解. 解:(1)画出函数的图象如图. ∵f(x)=-x2-2x+3=-(x+1)2+4的顶点为(-1,4), 又-1∈［-2,3］, ∴fmax=4. 又在x轴上,点3到点-1的距离比点-2到点-1的距离大, ∴fmin=f(3)=-(3+1)2+4=-12. ∴f(x)=-x2-2x+3(-2≤x≤3)的值域为［-12,4］. (2)画出函数的图象如下图. ∵f(x)=2x2-4x+3=2(x-1)2+1的顶点为(1,1), 又1 又在x轴上点3到点1的距离大于点2到点1的距离, ∴fmin=f(2)=2(2-1)2+1=3,fmax=f(3)=2(3-1)2+1=9. ∴f(x)=2x2-4x+3(2≤x≤3)的值域为［3,9］. 方法点拨 求二次函数的值域问题是高中数学的基本问题,也是重要问题.其基本解答步骤如下: (1)求顶点坐标,并判断顶点横坐标是否在给定区间上; (2)如果顶点横坐标在给定区间上,则最大(小)值为顶点纵坐标,最小(大)值为给定区间的两个端点横坐标中到顶点横坐标距离较大的对应函数值；如果不在给定区间上,则两个端点的函数值一个为最大,一个为最小.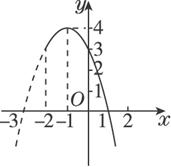
［2,3］,
经纶学典提高班系列答案
普通高中新课程问题导学案系列答案
名牌牛皮卷提优名卷系列答案
海淀黄冈全程大考卷系列答案
金榜1卷通系列答案
启东黄冈小状元系列答案
江苏正卷系列答案
悦然好学生周周测系列答案
单元加期末复习与测试系列答案