题目内容
已知6sin2α＋5sinαcosα－4cos2α＝0，α∈(
，2π)．
(1)求tanα的值；
(2)求cos(α＋
)的值．
(1)∵α∈(，2π)，∴cosα≠0，
∵6sin2α＋5sinαcosα－4cos2α＝0，
∴6tan2α＋5tanα－4＝0，
解得tanα＝－
或tanα＝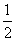
.
∵α∈(，2π)，∴tanα<0.
故tanα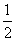＝(舍去)，∴tanα＝－.
(2)∵α∈(，2π)，∴由tanα＝－，
求得sinα＝－
，cosα＝
.
∴cos(α＋)＝cosαcos－sinαsin
＝×－(－)×
＝
.
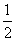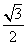练习册系列答案
相关题目
x，则tanα＝( )
B.
的值为( )
＝0的两根之和等于两根之积的一半，则△ABC一定是( )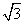
sinx－cosx，x∈R.若f(x)≥1，则x的取值范围为( )
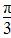≤x≤2kπ＋π，k∈Z}
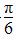≤x≤2kπ＋
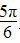，k∈Z}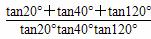
的值是________．