题目内容
已知关于x的方程x2-xcosA·cosB+2sin2 =0的两根之和等于两根之积的一半,则△ABC一定是( )
=0的两根之和等于两根之积的一半,则△ABC一定是( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.钝角三角形
C
[解析] 由题意得,cosAcosB=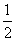 ·2sin2
·2sin2 ⇒
⇒
cosA·cosB= ⇒2cosA·cosB=1+cos(A+B)
⇒2cosA·cosB=1+cos(A+B)
⇒2cosA·cosB=1+cosA·cosB-sinA·sinB
⇒cosA·cosB+sinA·sinB=1⇒cos(A-B)=1⇒A-B=0⇒A=B,所以△ABC一定是等腰三角形,故选C.

练习册系列答案
相关题目
某同学利用描点法画函数y=Asin(ωx+φ)(其中A>0,0<ω<2,- <φ<
<φ< )的图象,列出的部分数据如下表:
)的图象,列出的部分数据如下表:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 0 | 1 | -1 | -2 |
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+φ)的解析式应是________.
有一段“三段论”推理是这样的:对于可导函数f(x),如果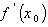 =0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值
=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值 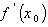 =0所以,x=0是函数f(x)=x3的极值点.以上推理中( )
=0所以,x=0是函数f(x)=x3的极值点.以上推理中( )
|
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
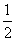 x2
x2 x2 D.y=
x2 D.y= x2
x2 ,则tanθ+
,则tanθ+ 的值是( )
的值是( ) =
= ,则sin2α=( )
,则sin2α=( ) B.
B. ,2π).
,2π). )的值.
)的值.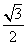 B.-
B.- ,
,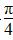 ]上是增函数,那么( )
]上是增函数,那么( ) B.0<ω≤2
B.0<ω≤2 D.ω≥2
D.ω≥2