题目内容
18．抛物线$y=\frac{1}{2}{x^2}$的焦点坐标是（ ）| A． | （0，1） | B． | $（{0，\frac{1}{2}}）$ | C． | $（{0，\frac{1}{4}}）$ | D． | $（{0，\frac{1}{8}}）$ |
分析 先根据标准方程求出p值，判断抛物线x2=2y的开口方向及焦点所在的坐标轴，从而写出焦点坐标．
解答 解：∵抛物线$y=\frac{1}{2}{x^2}$，即x2=2y中，p=1，$\frac{p}{2}$=$\frac{1}{2}$，焦点在y轴上，开口向上，
∴焦点坐标为（0，$\frac{1}{2}$），
故选：B．
点评 本题考查了抛物线的方程与几何性质，求解焦点坐标，属于容易题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
9．过点P（3，1）作圆x2+y2-2x=0的两条切线，切点分别为A，B，则直线AB的方程为（ ）
| A． | 2x-y-3=0 | B． | 2x+y-3=0 | C． | x-2y-3=0 | D． | x+2y-3=0 |
13．在直三棱柱ABC-A′B′C′中，所有的棱长都相等，M为B′C′的中点，N为A′B′的中点，则AM与BN所成角的余弦值为（ ）
| A． | $\frac{{2\sqrt{5}}}{7}$ | B． | $\frac{{\sqrt{35}}}{14}$ | C． | $-\frac{{2\sqrt{5}}}{7}$ | D． | $-\frac{{\sqrt{35}}}{14}$ |
3．若$\overrightarrow a=（{2sin2x，-1}），\overrightarrow b=（{{{sin}^2}x，sin2x}）$，且函数$f（x）=\overrightarrow a•\overrightarrow b$，则f（x）是（ ）
| A． | 最小正周期为$\frac{π}{2}$的奇函数 | B． | 最小正周期为π的奇函数 | ||
| C． | 最小正周期为$\frac{π}{2}$的偶函数 | D． | 最小正周期为π的偶函数 |
10．阅读如图程序框图，为使输出的数据为15，则①处应填的数字为（ ）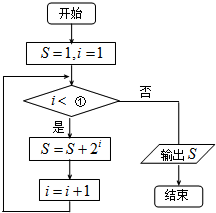
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |