题目内容
已知复数z1，z2满足|z1|=|z2|=1，|z1-z2|=
，则|z1+z2|等于（ ）
| 3 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、3 |
考点：复数求模
专题：计算题,数系的扩充和复数
分析：根据复数的运算法则，进行计算即可．
解答：
解：根据题意，
∵|z1|=|z2|=1，|z1-z2|=
，
∴|z1|2-2z1z2+|z2|2=3，
∴2z1z2=2-3=-1；
∴|z1+z2|=
=
=1．
故选：C．
∵|z1|=|z2|=1，|z1-z2|=
| 3 |
∴|z1|2-2z1z2+|z2|2=3，
∴2z1z2=2-3=-1；
∴|z1+z2|=
| |z1|2+2z1z2+|z2|2 |
| 1-1+1 |
故选：C．
点评：本题考查了复数求模的问题，复数的求模类似于向量的求模运算，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若直线l经过原点和点（
，-1），则直线l的倾斜角为（ ）
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
若复数z满足
=4-3i，则|z|等于（ ）
| (1-2i)2 |
| z |
| A、1 | ||
B、
| ||
| C、5 | ||
D、
|
设i是虚数单位，且i2014=
，则实数k=（ ）
| i-k |
| ki-1 |
| A、2 | B、1 | C、0 | D、-1 |
在△ABC中，已知a=6，b=9，∠A=45°，则这个三角形解的情况是（ ）
| A、有一个解 | B、有两个解 |
| C、无解 | D、不能确定 |
已知函数y=xf′（x）的图象如图所示，则y=f（x）的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
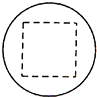已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是（ ）| A、64π | B、32π |
| C、16π | D、12π |