Question

如图所示，A，B，C是圆O上的三点，CO的延长线与线段BA的延长线交于圆O外的点D，若

OC

=m

OA

+n

OB

，则m+n的取值范围是

（-1，0）

．

Answer 1

分析：先利用向量数量积运算性质，将

OC

=m

OA

+n

OB

两边平方，消去半径得m、n的数量关系，利用向量加法的平行四边形法则，可判断m+n一定为负值，从而可得正确结果．

解答：解：∵|OC|=|OB|=|OA|，

OC

=m

OA

+n

OB

，
∴

OC

2=（m

OA

+n

OB

） 2=m²

OA

²+n²

OB

²+2mn

OA

•

OB

∴1=m²+n²+2mncos∠AOB
当∠AOB=60°时，m²+n²+mn=1，即（m+n）²-mn=1，即（m+n）²=1+mn＜1，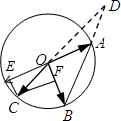
∴-1＜m+n＜1，当

OA

，

OB

趋近射线OD，由平行四边形法则

OC

=

OE

+

OF

═m

OA

+n

OB

，此时显然m＜0，n＞0，且|m|＞|n|，
∴m+n＜0，所以m+n的取值范围（-1，0）．
故答案为：（-1，0）．

点评：本题主要考查了平面向量的几何意义，平面向量加法的平行四边形法则，平面向量基本定理，平面向量数量积运算的综合运用，排除法解选择题，难度较大．