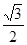题目内容
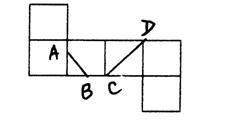
一个正方体的展开图如图所示，A、B、C、D为原正方体的顶点，则在原来的正方体中（ ）分析：以AB所在平面为正方体的后侧面，折起后得到正方体，求异面直线AB和CD所成的角．
解答：解：把正方体的展开图折起，如图，
连结BE，则CD∥BE，
∴AB和CD所成的角为∠ABE，
连结AE，则△ABE为正三角形，∴∠ABE=60°．
∴AB与CD所成的角为60°．
故选：C．
连结BE，则CD∥BE，
∴AB和CD所成的角为∠ABE，
连结AE，则△ABE为正三角形，∴∠ABE=60°．
∴AB与CD所成的角为60°．
故选：C．
点评：本题考查了异面直线及其所成的角，考查了学生的空间想象能力和思维能力，解答的关键是由展开图折回到原图形，是中档题．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
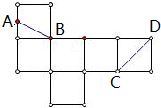一个正方体的展开图如图所示，B，C，D为原正方体的顶点，A为原正方体一条棱的中点．在原来的正方体中，CD与AB所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
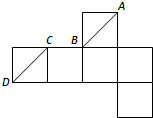一个正方体的展开图如图所示，A、B、C、D为原正方体的顶点，则在原来的正方体中（ ）
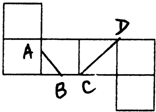一个正方体的展开图如图示，C、D为原正方体的顶点，AB为原正方体的棱的中点，在原正方体中，CD与AB所成角的余弦值为（ ）
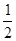C、
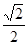D、
