题目内容
已知直线l的斜率为
，且经过点A（1，-1），
（1）求直线的l的方程（请给出一般式），
（2）求以N（1，3）为圆心，并且与直线l相切的圆的方程．
| 3 | 4 |
（1）求直线的l的方程（请给出一般式），
（2）求以N（1，3）为圆心，并且与直线l相切的圆的方程．
分析：（1）根据直线l的斜率以及A坐标，表示出直线l方程，整理即可得到结果；
（2）利用点到直线的距离公式求出N到直线l的距离，即为圆的半径，写出圆的方程即可．
（2）利用点到直线的距离公式求出N到直线l的距离，即为圆的半径，写出圆的方程即可．
解答：解：（1）直线l经过点A（1，-1），斜率为
，
∴由点斜式方程可得y+1=
（x-1），把它化为一般式为3x-4y-7=0；
（2）∵点N（1，3）到直线3x-4y-7=0的距离d=
=
，
则所求的圆的方程是（x-1）2+（y-3）2=
．
| 3 |
| 4 |
∴由点斜式方程可得y+1=
| 3 |
| 4 |
（2）∵点N（1，3）到直线3x-4y-7=0的距离d=
| |3-4×3-7| |
| 5 |
| 16 |
| 5 |
则所求的圆的方程是（x-1）2+（y-3）2=
| 256 |
| 25 |
点评：此题考查了圆的标准方程，直线的点斜式方程，以及直线的一般式方程，直线与圆相切时圆心到切线的距离等于圆的半径，熟练掌握此性质是解本题的关键．
练习册系列答案
相关题目
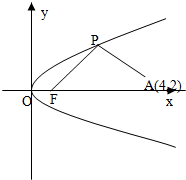如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．