题目内容

已知直线l的斜率为
16
，且和坐标轴围成面积为3的三角形，求直线l的方程．
分析：设出直线方程的斜截式方程，求出直线在两条坐标轴上的截距，利用三角形的面积公式求解直线在y轴上的截距，从而可得答案．
解答：解：设直线l的方程为y=
1
6
x+m，
取y=0，得x=-6m．
所以l和坐标轴围成面积为S=
1
2
|m||-6m|=3．
解得m=±1．
所以直线l的方程为y=
1
6
x±1，即x-6y±6=0．
点评：本题考查了直线方程的一般式，训练了斜截式和一般式的互化，是基础题．
练习册系列答案
相关题目
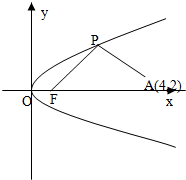精英家教网如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．
（1）求|PA|+|PF|的最小值；
（2）求k的取值范围；
（3）若O为坐标原点，问是否存在点M，使过点M的动直线与抛物线交于B，C两点，且以BC为直径的圆恰过坐标原点，若存在，求出动点M的坐标；若不存在，请说明理由．
已知直线l的斜率为2，且过点A（-1，-2），B（3，m），则m的值为（　　）
已知直线l的斜率k=1-m2（m∈R），则倾斜角θ的取值范围为
[0，
π
4
]∪（
π
2
，π）
[0，
π
4
]∪（
π
2
，π）
．
（2007•肇庆二模）已知直线l的斜率为k=-1，经过点M0（2，-1），点M在直线上，以
M0M
的数量t为参数，则直线l的参数方程为
x=2-
2
2
t
y=-1+
2
2
t
(t为参数)
x=2-
2
2
t
y=-1+
2
2
t
(t为参数)
．
已知直线l的斜率为-1．
（1）若直线l过点（2，2），求直线l的方程；
（2）若直线l与坐标轴所围成的三角形的面积是12，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网