题目内容
(本小题满分14分)已知函数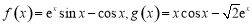 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数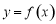 在
在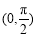 内的零点的个数,并说明理由;
内的零点的个数,并说明理由;
(Ⅱ)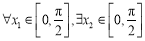 ,使得不等式
,使得不等式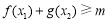 成立,试求实数
成立,试求实数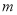 的取值范围;
的取值范围;
(Ⅲ)若 ,求证:
,求证: .
.
(Ⅰ)函数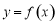 在
在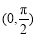 上的零点的个数为1; (Ⅱ)
上的零点的个数为1; (Ⅱ)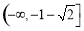 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)因为 ,所以
,所以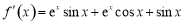 .因为
.因为 ,所以
,所以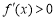 ,所以函数
,所以函数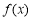 在
在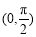 上是单调递增函数.因为
上是单调递增函数.因为 ,
,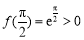 ,根据函数零点存在性定理得函数
,根据函数零点存在性定理得函数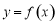 在
在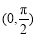 上的零点的个数为1.(Ⅱ)因为不等式
上的零点的个数为1.(Ⅱ)因为不等式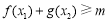 等价于
等价于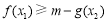 ,所以
,所以 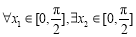 ,使得不等式
,使得不等式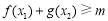 成立,等价于
成立,等价于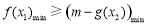 ,即
,即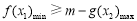 .利用导数,解不等式即可求出结果;(Ⅲ)采用分析证明发,利用导数在函数单调性中的应用,以及直线与圆的位置关系即可求证结论.
.利用导数,解不等式即可求出结果;(Ⅲ)采用分析证明发,利用导数在函数单调性中的应用,以及直线与圆的位置关系即可求证结论.
试题解析:【解析】
(Ⅰ)函数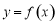 在
在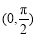 上的零点的个数为1. 1分
上的零点的个数为1. 1分
理由如下:
因为 ,所以
,所以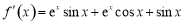 . 2分
. 2分
因为 ,所以
,所以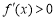 ,
,
所以函数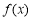 在
在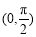 上是单调递增函数. 3分
上是单调递增函数. 3分
因为 ,
,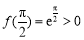 ,
,
根据函数零点存在性定理得
函数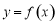 在
在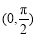 上的零点的个数为1. 4分
上的零点的个数为1. 4分
(Ⅱ)因为不等式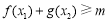 等价于
等价于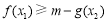 ,
,
所以 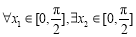 ,使得不等式
,使得不等式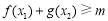 成立,等价于
成立,等价于
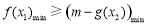 ,即
,即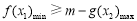 . 6分
. 6分
当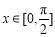 时,
时,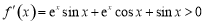 ,故
,故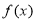 在区间
在区间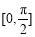 上单调递增,所以
上单调递增,所以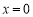 时,
时,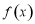 取得最小值
取得最小值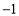 . 7分
. 7分
又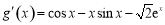 ,由于
,由于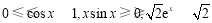 ,
,
所以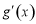
 ,故
,故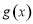 在区间
在区间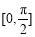 上单调递减,
上单调递减,
因此,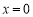 时,
时,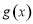 取得最大值
取得最大值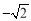 . 8分
. 8分
所以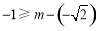 ,所以
,所以 .
.
所以实数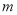 的取值范围是
的取值范围是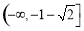 . 9分
. 9分
(Ⅲ)当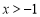 时,要证
时,要证 ,只要证
,只要证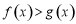 ,
,
只要证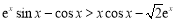 ,
,
只要证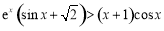 ,
,
由于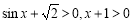 ,只要证
,只要证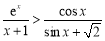 . 10分
. 10分
下面证明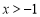 时,不等式
时,不等式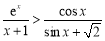 成立.
成立.
令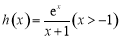 ,则
,则 ,
,
当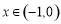 时,
时,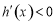 ,
,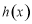 单调递减;
单调递减;
当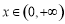 时,
时,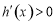 ,
,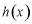 单调递增.
单调递增.
所以当且仅当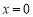 时,
时,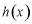 取得极小值也就是最小值为1.
取得极小值也就是最小值为1.
令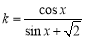 ,其可看作点
,其可看作点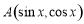 与点
与点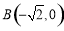 连线的斜率,
连线的斜率,
所以直线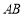 的方程为:
的方程为: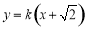 ,
,
由于点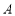 在圆
在圆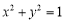 上,所以直线
上,所以直线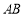 与圆
与圆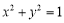 相交或相切,
相交或相切,
当直线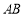 与圆
与圆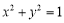 相切且切点在第二象限时,
相切且切点在第二象限时,
直线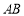 取得斜率
取得斜率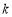 的最大值为
的最大值为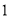 . 12分
. 12分
故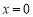 时,
时,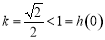 ;
;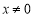 时,
时,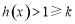 . 13分
. 13分
综上所述,当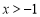 时,
时, 成立. 14分.
成立. 14分.
考点:1.利用导数判断函数的单调性;2.导数在不等式证明中的应用;3.恒成立问题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
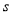 的值为( )
的值为( )
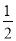 B.
B.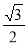 C.
C.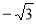 D.0
D.0  若z=y-ax取得最大值的最优解不唯一,则实数a的值为
若z=y-ax取得最大值的最优解不唯一,则实数a的值为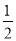 或-1 B.2或
或-1 B.2或 C.2或1 D.2或-1
C.2或1 D.2或-1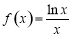 ,有下列四个命题:
,有下列四个命题: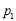 :
: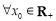 ,
, ,
,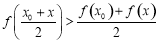 ;
; :
: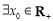 ,
,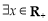 ,
, ;
;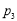 :
: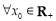 ,
,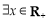 ,
, ;
;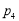 :
: ,
,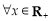 ,
, .
.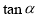
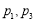 B.
B.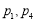 C.
C.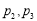 D.
D.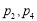
 ”是“
”是“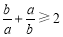 ”的( ).
”的( ). 的公比
的公比 ,
, ,
,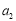 是方程
是方程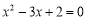 的两根.
的两根.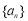 的通项公式;
的通项公式;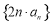 的前
的前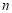 项和
项和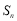 .
. ”为:
”为: .若函数
.若函数 ,则该函数的图象大致是( ).
,则该函数的图象大致是( ).
 在
在 上为减函数,则实数
上为减函数,则实数 的值是 .
的值是 . 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱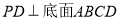 ,
,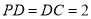 ,
,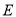 是
是 的中点,
的中点,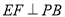 交
交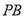 于点
于点 .
.
 //平面
//平面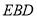 ;
;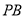 ⊥平面
⊥平面 ;
;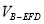 .
.