题目内容
某园林局对1000株树木的生长情况进行调查,其中槐树600株,银杏树400株.现用分层抽样方法从这1000株树木中随机抽取100株,其中银杏树树干周长(单位:cm)的抽查结果如下表:
则x的值为
.
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 株数 | 4 | 18 | x | 6 |
12
12
;若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.则排查的树木恰好为2株的概率为| 1 |
| 4 |
| 1 |
| 4 |
分析:对于第一问,根据题意,计算可得分层抽样的比例,进而由银杏树的数目,可得要抽取的银杏树的棵树,根据题干中的表格,计算可得答案;对于第二问,试验发生包含的事件是恰好在排查到第二株时发现患虫害树,可以列举出所有的基本事件,同时可得满足条件的事件数目,由等可能事件的概率计算可得答案.
解答:解:根据题意,用分层抽样方法从这1000株树木中随机抽取100株,则应该抽取银杏100×
=40株
即表中应有4+18+x+6=40,
则x=40-4-18-16=12;
记这4株树为树1,树2,树3,树4,且设树1为患虫害的树,
记恰好在排查到第二株时发现患虫害树为事件A,则A是指第二次排查到的是树1
从4棵树中先后取出2棵,其基本事件有:
(树1,树2),(树1,树3),(树1,树4),(树2,树1),(树2,树3),(树2,树4)
(树3,树1),(树3,树2),(树3,树4),(树4,树1),(树4,树2),(树4,树3);共12个基本事件,
而事件A中包含的基本事件有3个
所以恰好在排查到第二株时发现患虫害的概率P(A)=
=
故答案为12;
.
| 400 |
| 1000 |
即表中应有4+18+x+6=40,
则x=40-4-18-16=12;
记这4株树为树1,树2,树3,树4,且设树1为患虫害的树,
记恰好在排查到第二株时发现患虫害树为事件A,则A是指第二次排查到的是树1
从4棵树中先后取出2棵,其基本事件有:
(树1,树2),(树1,树3),(树1,树4),(树2,树1),(树2,树3),(树2,树4)
(树3,树1),(树3,树2),(树3,树4),(树4,树1),(树4,树2),(树4,树3);共12个基本事件,
而事件A中包含的基本事件有3个
所以恰好在排查到第二株时发现患虫害的概率P(A)=
| 3 |
| 12 |
| 1 |
| 4 |
故答案为12;
| 1 |
| 4 |
点评:本题考查排列、组合以及分类计数原理的应用,关键要掌握分层抽样方法和理解表格的意义.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
某园林局对1000株树木的生长情况进行调查,其中槐树600株,银杏树400株.现用分层抽样方法从这1000株树木中随机抽取100株,其中银杏树树干周长(单位:cm)的抽查结果如下表:
(1)求x的值;
(2)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 株数 | 4 | 18 | x | 6 |
(2)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
(本小题满分12分)
某园林局对1000株树木的生长情况进行调查,其中杉树 600株,槐树400株 .现用分层抽样方法从这1000株树木中随机抽取100株,杉树与槐树的树干周长(单位:cm)的抽查结果如下表:
|
树干周长 (单位:cm ) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
|
杉 树 |
6 |
19 |
21 |
|
|
槐 树 |
4 |
20 |
|
6 |
(I)求 ,
, 值及估计槐树树干周长的众数;
值及估计槐树树干周长的众数;
(Ⅱ)如果杉树的树干周长超过60cm就可以砍伐,请估计该片园林可以砍伐的杉树有多少株?
(Ⅲ)树干周长在30cm到40cm之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
(本小题满分13分)
某园林局对1000株树木的生长情况进行调查,其中槐树600株,银杏树400株. 现用分层抽样方法从这1000株树木中随机抽取100株,其中银杏树树干周长(单位:cm)的抽查结果如下表:
|
树干周长(单位:cm) |
|
|
|
|
|
株数 |
4 |
18 |
|
6 |
(I)求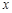 的值 ;
的值 ;
(II)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
(12分)某园林局对1000株树木的生长情况进行调查,其中槐树600株,银杏树400株. 现用分层抽样方法从这1000株树木中随机抽取100株,其中银杏树树干周长(单位:cm)的抽查结果如下表:
|
树干周长(单位:cm) |
|
|
|
|
|
株数 |
4 |
18 |
|
6 |
(I)求 的值 ;
的值 ;
(II)若已知树干周长在30cm至40cm之间的4株银杏树中有1株患有虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.







