题目内容
14.当a>0且a≠1时,函数y=(1-a)x与函数y=logax在同一坐标系内的图象可能是( )| A. | 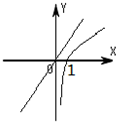 | B. | 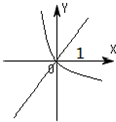 | C. | 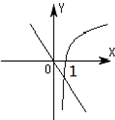 | D. | 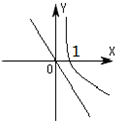 |
分析 由函数y=(1-a)x与函数y=logax的解析式,分情况讨论两函数的单调性,根据对数的图象和性质即可得解.
解答 解:由于a>0且a≠1,
所以可得:①当a>1时,y=logax为过点(1,0)的增函数,1-a<0,函数y=(1-a)x为减函数;
②当0<a<1时,y=logax为过点(1,0)减函数,1-a>0,函数y=(1-a)x为增函数;
故选:C.
点评 本题考查对数函数的图象与性质,着重考查一次函数y=(1-a)x与对数函数y=logax之间的对应关系,考查数形结合的分析能力,属于中档题.

练习册系列答案
相关题目
18.已知tan(α+β-$\frac{π}{4}$)=$\frac{1}{2}$,tan(β-$\frac{π}{4}$)=-$\frac{1}{3}$,则tan(α+$\frac{π}{3}$)=( )
| A. | $\sqrt{3}$-2 | B. | 2-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | -2-$\sqrt{3}$ |
2.已知函数$f(x)=\left\{{\begin{array}{l}{cosx-1,x≤0}\\{{{sin}^2}x,x>0}\end{array}}\right.$,则下列结论正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是单调函数 | C. | f(x)是周期函数 | D. | f(x)的值域为[-2,1] |
6.“?x∈R,ex-2>m”是“m2>2”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
3.已知数列$\sqrt{3}$,$\sqrt{5}$,$\sqrt{7}$,$\sqrt{11}$,…,$\sqrt{2n+1}$,…,则5是这个数列的( )
| A. | 第12项 | B. | 第13项 | C. | 第14项 | D. | 第25项 |