题目内容
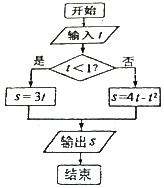
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
【答案】
(1)
(0.0) (![]() ,
,![]() )
)
(2)
4
【解析】(1)曲线C2的直角坐标方程为x2+y2-2y=0,曲线C3 的直角坐标方程分别为x2+y2-2![]() x=0,联立两方程组解可得
x=0,联立两方程组解可得![]() 或
或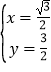 , 所以C2与C3得交点直角坐标为(0.0) (
, 所以C2与C3得交点直角坐标为(0.0) (![]() ,
,![]() )。
)。
(2)曲线C1极坐标方程为![]() =
=![]() (
(![]()
![]() R,
R,![]() ≠0),其中0
≠0),其中0![]()
![]()
![]() , 因此点A的极坐标为(2sin
, 因此点A的极坐标为(2sin![]() ,
, ![]() ),点B的极坐标为 (2
),点B的极坐标为 (2![]() cos
cos![]() ,
, ![]() ),所以|AB|=|2sin
),所以|AB|=|2sin![]() -2
-2![]() cos
cos![]() |=4|sin(
|=4|sin(![]() -
-![]() )|,当
)|,当![]() =
=![]() 时,|AB|取得最大值,最大值为4。
时,|AB|取得最大值,最大值为4。
【考点精析】根据题目的已知条件,利用参数方程的定义的相关知识可以得到问题的答案,需要掌握在平面直角坐标系中,如果曲线上任意一点的坐标![]() 都是某个变数
都是某个变数![]() 的函数
的函数![]() 并且对于
并且对于![]() 的每一个允许值,由这个方程所确定的点
的每一个允许值,由这个方程所确定的点![]() 都在这条曲线上,那么这个方程就叫做这条曲线的参数方程.
都在这条曲线上,那么这个方程就叫做这条曲线的参数方程.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目