题目内容
P、Q、M、N四点都在椭圆x2+
分析:由已知得![]() ⊥
⊥![]() ,故可设出直线PF的方程,求出弦长|PQ|.同理可求弦长|MN|,然后建立起目标函数即可求出最大、最小值.
,故可设出直线PF的方程,求出弦长|PQ|.同理可求弦长|MN|,然后建立起目标函数即可求出最大、最小值.
解:如图,由条件知MN和PQ 是椭圆的两条弦,相交于焦点F(0,1),且PQ⊥MN,直线PQ、NM中至少有一条存在斜率,不妨设PQ的斜率为k,
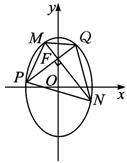
又PQ过点F(0,1),故PQ的方程为y=kx+1.
将此式代入椭圆方程得(2+k2)x2+2kx-1=0.
设P、Q两点的坐标分别为(x1,y1),(x2,y2),则x1=![]() ,x2=
,x2=![]() .
.
从而|PQ|2=(x1-x2)2+(y1-y2)2=![]() ,
,
亦即|PQ|=![]() .
.
(ⅰ)当k≠0时,MN的斜率为-![]() ,同上可推得
,同上可推得
|MN|=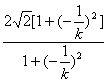 .
.
故四边形PMQN的面积
S=![]() |PQ|·|MN|
|PQ|·|MN|
=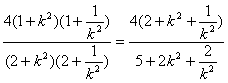 .
.
令u=k2+![]() ,得
,得
S=![]() =2(1-
=2(1-![]() ).
).
因为u=k2+![]() ≥2,
≥2,
当k=±1时,u=2,S=![]() ,
,
且S是以u为自变量的增函数,
所以![]() ≤S<2.
≤S<2.
(ⅱ)当k=0时,MN为椭圆长轴,|MN|=2![]() ,|PQ|=
,|PQ|=![]() ,S=
,S=![]() |PQ|·|MN|=2.
|PQ|·|MN|=2.
综合(ⅰ)(ⅱ)知,四边形PMQN面积的最大值为2,最小值为![]() .
.

练习册系列答案
相关题目
 上,F为椭圆在y轴正半轴上的焦点.已知
上,F为椭圆在y轴正半轴上的焦点.已知 与
与 共
共 与
与 共线.求四边形PMQN的面积的最小值和最大值.
共线.求四边形PMQN的面积的最小值和最大值.