题目内容
(本小题满分12分)
P、Q、M、N四点都在椭圆 上,F为椭圆在y轴正半轴上的焦点.已知
上,F为椭圆在y轴正半轴上的焦点.已知 与
与 共
共
线,且 与
与 共线.求四边形PMQN的面积的最小值和最大值.
共线.求四边形PMQN的面积的最小值和最大值.
【答案】
解:如图,由条件知MN和PQ是椭圆的两条弦,相交于焦点F(0,1),且PQ⊥MN,直线PQ、NM中至少有一条存在斜率,不妨设PQ的斜率为 .
.
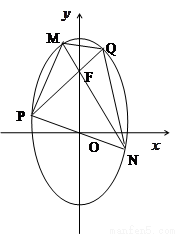
又PQ过点F(0,1),故PQ的方程为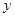 =
=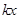 +1
+1
将此式代入椭圆方程得(2+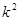 )
)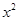 +2
+2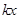 -1=0
-1=0
设P、Q两点的坐标分别为( ,
,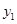 ),(
),(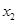 ,
,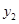 ),
),
则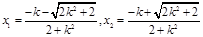
从而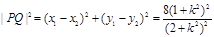
亦即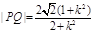 .…………………………………4分
.…………………………………4分
①当 ≠0时,MN的斜率为-
≠0时,MN的斜率为-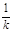 ,同上可推得
,同上可推得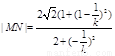
故四边形面积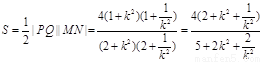
令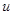 =
=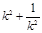 得
得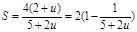 .…………………………………8分
.…………………………………8分
∵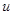 =
=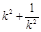 ≥2 .当
≥2 .当 =±1时
=±1时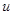 =2,S=
=2,S=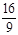 且S是以
且S是以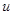 为自变量的增函数.∴
为自变量的增函数.∴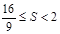 .
.
②当 =0时,MN为椭圆长轴,|MN|=2
=0时,MN为椭圆长轴,|MN|=2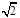 ,|PQ|=
,|PQ|=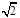 . ∴S=
. ∴S=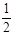 |PQ||MN|=2.
|PQ||MN|=2.
综合①②知四边形PMQN的最大值为2,最小值为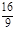 .………………………………12分
.………………………………12分
【解析】略

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目