题目内容
9.已知函数f(x)=x|x-m|(m∈R),g(x)=logax.(1)若关于x的不等式f(x)≤2的解集恰好为(-∞,t],求实数t的最大值;
(2)当m=0时,集合A={x|f(x)<g(x)},集合B=(0,$\frac{1}{2}$),且A⊆B,求a的取值范围.
分析 (1)易知t>0,且可知当t取得最大值时,则m也取得最大值;从而转化为求m的最大值,再求t;
(2)由题意得x2<logax,从而讨论可得$\frac{1}{2}$2≥loga$\frac{1}{2}$,从而解得.
解答 解:(1)当x≤0时,f(x)=x|x-m|≤0,
故t>0,
故t|t-m|=2,
∵t=m时,t|t-m|=0,
∴t>m,
故t(t-m)=2,
故m=t-$\frac{2}{t}$,
故m=t-$\frac{2}{t}$在(0,+∞)上是增函数,
故求t的最大值,则m也取得最大值;
而当m>0时,f(x)=x|x-m|的图象如下,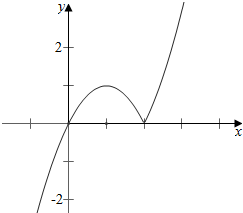 ,
,
故$\frac{m}{2}$•$\frac{m}{2}$≤2,
故m≤2$\sqrt{2}$,
故当m=2$\sqrt{2}$时,
故t(t-2$\sqrt{2}$)≤2,
解得,2$\sqrt{2}$≤t≤2+$\sqrt{2}$,
故实数t的最大值为2+$\sqrt{2}$;
(2)由题意得,x|x|<logax,
即x2<logax,
∵x2>0,且不等式的解集A⊆(0,$\frac{1}{2}$),
∴存在x∈(0,$\frac{1}{2}$),logax>0,
故a<1,
当0<a<1时,y=logax是减函数,而y=x2在(0,$\frac{1}{2}$)上是增函数,
故$\frac{1}{2}$2≥loga$\frac{1}{2}$,
即0<a≤$\frac{1}{16}$;
故a的取值范围为(0,$\frac{1}{16}$].
点评 本题考查了分类讨论的思想应用及转化思想的应用,同时考查了函数与不等式的关系应用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.已知函数f(x)=$\frac{9x}{1+a{x}^{2}}$(a>0),则f(x)在[$\frac{1}{2}$,2]上的最大值为( )
| A. | 0 | B. | $\frac{18}{4a+1}$ | ||
| C. | $\frac{18}{a+4}$或$\frac{18}{4a+1}$ | D. | $\frac{18}{4a+1}$或$\frac{18}{a+4}$或$\frac{9\sqrt{a}}{2a}$ |
17.已知集合A={0,1,2},B={2,3},则集合A∪B=( )
| A. | {1,2,3} | B. | {0,1,2,3} | C. | {2} | D. | {0,1,3} |
14.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,2),k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$平行,则k的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
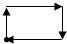
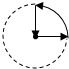
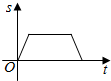 如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )
如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )
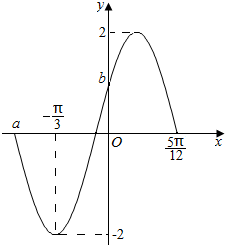 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.