题目内容
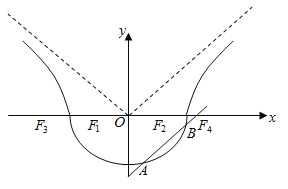
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)①求函数![]() 的单调区间;
的单调区间;
②若![]() 满足
满足![]() ,且
,且![]() .求证:
.求证:![]() .
.
(2)函数![]() .若
.若![]() 对任意,
对任意,![]() 都有
都有![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)①单调递增区间![]() ,
,![]() ,单调递减区间
,单调递减区间![]() ;②详见解析;(2)
;②详见解析;(2)![]() .
.
【解析】
(1)①求导可得![]() ,再分别求解
,再分别求解![]() 与
与![]() 的解集,结合定义域分析函数的单调区间即可.
的解集,结合定义域分析函数的单调区间即可.
②根据(1)中的结论,求出![]() 的表达式,再分
的表达式,再分![]() 与
与![]() 两种情况,结合函数的单调性分析
两种情况,结合函数的单调性分析![]() 的范围即可.
的范围即可.
(2)求导分析![]() 的单调性,再结合
的单调性,再结合![]() 单调性,设
单调性,设![]() 去绝对值化简可得
去绝对值化简可得![]() ,再构造函数
,再构造函数![]() ,
,![]() ,根据函数的单调性与恒成立问题可知
,根据函数的单调性与恒成立问题可知![]() ,再换元表达
,再换元表达![]() 求解最大值即可.
求解最大值即可.
解:![]() ,
,
由![]() 可得
可得![]() 或
或![]() ,
,
由![]() 可得
可得![]() ,
,
故函数的单调递增区间![]() ,
,![]() ,单调递减区间
,单调递减区间![]() ;
;
![]() ,
,
![]() 或
或![]() ,
,
若![]() ,因为
,因为![]() ,故
,故![]() ,
,![]() ,
,
由![]() 知
知![]() 在
在![]() 上单调递增,
上单调递增,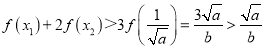 ,
,
若![]() 由
由![]() 可得
可得![]() x1,
x1,
因为![]() ,
,
所以![]() ,
,
由![]() 在
在![]() 上单调递增,
上单调递增,
![]()
综上![]() .
.
![]()
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
不妨设![]()
由(1)![]() 在
在![]() 上单调递减,
上单调递减,
由![]() ,
,
可得![]() ,
,
所以![]() ,
,
令![]() ,
,![]() ,
,
可得![]() 单调递减,
单调递减,
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 的最大值
的最大值![]() .
.

练习册系列答案
相关题目
【题目】保护环境就是保护人类健康.空气中负离子浓度(单位:个/![]() )可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表
)可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表![]() .
.
表![]() 负离子浓度与空气质量对应标准:
负离子浓度与空气质量对应标准:
负离子浓度 | 等级 | 和健康的关系 |
|
| 不利 |
|
| 正常 |
|
| 较有利 |
|
| 有利 |
|
| 相当有利 |
|
| 很有利 |
|
| 极有利 |
图![]() 空气负离子浓度
空气负离子浓度
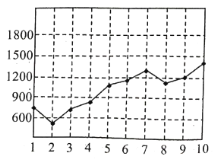
某地连续![]() 天监测了该地空气负离子浓度,并绘制了如图
天监测了该地空气负离子浓度,并绘制了如图![]() 所示的折线图.根据折线图,下列说法错误的是( )
所示的折线图.根据折线图,下列说法错误的是( )
A.这![]() 天的空气负离子浓度总体越来越高
天的空气负离子浓度总体越来越高
B.这![]() 天中空气负离子浓度的中位数约
天中空气负离子浓度的中位数约![]() 个
个![]()
C.后![]() 天的空气质量对身体健康的有利程度明显好于前
天的空气质量对身体健康的有利程度明显好于前![]() 天
天
D.前![]() 天空气质量波动程度小于后
天空气质量波动程度小于后![]() 天
天