Question

20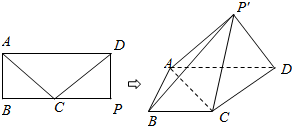．已知矩形ABPD，点C为BP的中点，AD=2，AB=1，将△CDP沿CD折起成四棱锥P′-ABCD，其中∠AP′D=90°
（1）求证：AC⊥平面P′CD；
（2）求CD与平面AP′D所成角的正弦值．

Answer 1

分析 （1）证明AC⊥CD和AC⊥P′D，即可证明AC⊥平面P′CD；
（2）找出CD与平面AP′D所成的角，利用等积法求出点C到平面AP′D的距离，即可求出CD与平面AP′D所成角的正弦值．

解答 解：（1）证明：矩形ABPD中，点C为BP的中点，AD=2，AB=1，
∴AC=DC=$\sqrt{2}$，
∴AC²+CD²=AD²，
∴AC⊥CD；
又∠AP′D=90°，∴P′D⊥AP′，
又P′D⊥P′C，且P′C∩P′A=P′，
AP′?平面ACP′，P′C?平面ACP′，
∴P′D⊥平面ACP′；
又AC?平面ACP′，
∴P′D⊥AC；
又P′D∩CD=D，P′D?平面P′CD，CD?平面P′CD，
∴AC⊥平面P′CD；
（2）如图所示，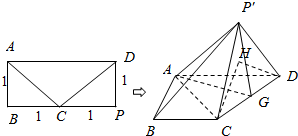

由（1）知，AC⊥平面CP′D，
AC?平面ACD，∴平面ACD⊥平面CP′D；
取CD的中点G，连接P′G，
则P′G⊥CD，
又平面ACD∩平面CP′D=CD，
P′G?平面CP′D，
∴P′G⊥平面ACD；
∴P′G=$\sqrt{{1}^{2}{-（\frac{\sqrt{2}}{2}）}^{2}}$=$\frac{\sqrt{2}}{2}$，；
设CH⊥平面AP′D，垂足为H，连接DH，则∠CDH为直线CD与平面AP′D所成的角，
由三棱锥的体积相等，得出
S_△AP′D•CH=S_△ACD•P′G，
即$\frac{1}{2}$•1•$\sqrt{3}$•CH=$\frac{1}{2}$•$\sqrt{2}$•$\sqrt{2}$•$\frac{\sqrt{2}}{2}$，
解得CH=$\frac{\sqrt{6}}{3}$；
∴sin∠CDH=$\frac{CH}{CD}$=$\frac{\frac{\sqrt{6}}{3}}{\sqrt{2}}$=$\frac{\sqrt{3}}{3}$，
即CD与平面AP′D所成角的正弦值为$\frac{\sqrt{3}}{3}$．

点评 本题考查了直线与平面垂直的判断与性质，以及直线与平面所成的角的应用问题，求直线与平面所成的角时找角是关键，是中档题目．