题目内容
已知函数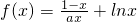 (1)若函数f(x)在[1,+∞)上为增函数,求正实数a的取值范围;(2)讨论函数f(x)的单调性;(3)当a=1时,求证:对大于1的任意正整数n,都有
(1)若函数f(x)在[1,+∞)上为增函数,求正实数a的取值范围;(2)讨论函数f(x)的单调性;(3)当a=1时,求证:对大于1的任意正整数n,都有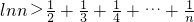 .
.
解:(1)∵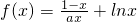 ∴f'(x)=
∴f'(x)=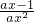 (a>0)…1
(a>0)…1
∵函数f(x)在[1,+∞)上为增函数∴f'(x)=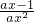 ≥0对x∈[1,+∞)恒成立
≥0对x∈[1,+∞)恒成立
ax-1≥0对x∈[1,+∞)恒成立,即a≥ 对x∈[1,+∞)恒成立∴a≥1 (4分)
对x∈[1,+∞)恒成立∴a≥1 (4分)
(2)∵a≠0 ,
,
当a<0时,f'(x)>0对x∈(0,+∞)恒成立,∴f(x)的增区间为(0,+∞)…5
当a>0时, ,
,
∴f(x)的增区间为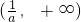 ,减区间为(
,减区间为( )…6
)…6
(3)当a=1时,f(x)= ,f'(x)=
,f'(x)= ,故f(x)在[1,+∞)上为增函数.
,故f(x)在[1,+∞)上为增函数.
当n>1时,令x= ,则x>1,故f(x)>f(1)=0…8
,则x>1,故f(x)>f(1)=0…8
∴f( )=
)=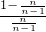 +
+ =-
=- +
+ >0,即
>0,即 >
>
∴lnn> +
+ +…+ln
+…+ln >
> +
+ +
+ +…+
+…+
分析:(1)函数f(x)在[1,+∞)上为增函数则f'(x)≥0对x∈[1,+∞)恒成立,建立关系式,解之即可;
(2)求出f(x)的导函数,化简整理后,根据a小于0和a大于0,分别讨论导函数的正负即可得到函数的单调区间;
(3)先研究函数f(x)在[1,+∞)上的单调性,令x= ,易得
,易得 >
> ,然后利用lnn>
,然后利用lnn> +
+ +…+ln
+…+ln 即可证得结论.
即可证得结论.
点评:此题考查学生会根据导函数的正负判断得到函数的单调区间,会根据函数的增减性证明不等式,是一道综合题.
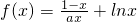 ∴f'(x)=
∴f'(x)=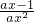 (a>0)…1
(a>0)…1∵函数f(x)在[1,+∞)上为增函数∴f'(x)=
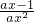 ≥0对x∈[1,+∞)恒成立
≥0对x∈[1,+∞)恒成立ax-1≥0对x∈[1,+∞)恒成立,即a≥
 对x∈[1,+∞)恒成立∴a≥1 (4分)
对x∈[1,+∞)恒成立∴a≥1 (4分)(2)∵a≠0
 ,
,当a<0时,f'(x)>0对x∈(0,+∞)恒成立,∴f(x)的增区间为(0,+∞)…5
当a>0时,
 ,
,
∴f(x)的增区间为
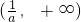 ,减区间为(
,减区间为( )…6
)…6(3)当a=1时,f(x)=
 ,f'(x)=
,f'(x)= ,故f(x)在[1,+∞)上为增函数.
,故f(x)在[1,+∞)上为增函数.当n>1时,令x=
 ,则x>1,故f(x)>f(1)=0…8
,则x>1,故f(x)>f(1)=0…8∴f(
 )=
)=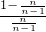 +
+ =-
=- +
+ >0,即
>0,即 >
>
∴lnn>
 +
+ +…+ln
+…+ln >
> +
+ +
+ +…+
+…+
分析:(1)函数f(x)在[1,+∞)上为增函数则f'(x)≥0对x∈[1,+∞)恒成立,建立关系式,解之即可;
(2)求出f(x)的导函数,化简整理后,根据a小于0和a大于0,分别讨论导函数的正负即可得到函数的单调区间;
(3)先研究函数f(x)在[1,+∞)上的单调性,令x=
 ,易得
,易得 >
> ,然后利用lnn>
,然后利用lnn> +
+ +…+ln
+…+ln 即可证得结论.
即可证得结论.点评:此题考查学生会根据导函数的正负判断得到函数的单调区间,会根据函数的增减性证明不等式,是一道综合题.

练习册系列答案
相关题目

 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围; .
.