Question

【题目】若函数图象上存在两个点A，B关于原点对称，则点对称为函数的“友好点对”且点对与可看作同一个“友好点对”若函数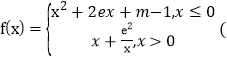其中e为自然对数的底数，恰好有两个“友好点对”则实数m的取值范围为　　

A. B. C. D.

Answer 1

【答案】C

【解析】

求出当时关于原点对称的函数，条件转化为当时，与的图象恰好有两个不同的交点，求函数的导数研究函数的单调性和最值，利用数形结合建立不等式关系进行求解即可．

解：当时，关于原点对称的函数为，

即，，

设，，

条件等价为当时，与的图象恰好有两个不同的交点，

则，，

当时，函数取得最大值，

当时，，．

由得，此时为增函数，

由得，此时为减函数，

即当时，函数取得极小值同时也是最小值，

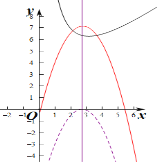
作出当时，与的图象如图：

要使两个图象恰好有两个不同的交点，

则，即，

即，

即，

故选：C．