题目内容
已知{an}是公差为d的等差数列,它的前n项和为Sn,S4=2S2+8.
(1)求公差d的值;
(2)若a1=1,设Tn是数列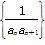 的前n项和,求使不等式Tn≥
的前n项和,求使不等式Tn≥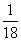 (m2-5m)对所有的n∈N*恒成立的最大正整数m的值;
(m2-5m)对所有的n∈N*恒成立的最大正整数m的值;
(3)设bn=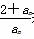 若对任意的n∈N*,都有bn≤b4成立,求a1的取值范围.
若对任意的n∈N*,都有bn≤b4成立,求a1的取值范围.
解:(1)设数列{an}的公差为d,
∵S4=2S2+8,即4a1+6d=2(2a1+d)+8,化简得:4d=8,
解得d=2.
(2)由a1=1,d=2,得an=2n-1,
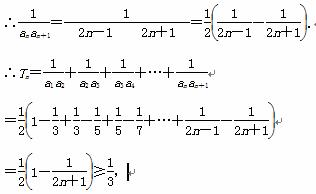 又∵不等式Tn≥
又∵不等式Tn≥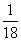 (m2-5m)对所有的n∈N*恒成立,
(m2-5m)对所有的n∈N*恒成立,
∴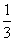 ≥
≥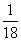 (m2-5m),
(m2-5m),
化简得:m2-5m-6≤0,解得:-1≤m≤6.
∴m的最大正整数值为6.
(3)由d=2,得an=a1+2n-2,
又∵bn=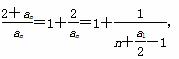
又函数f(x)=1+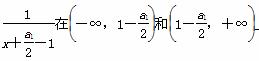 上分别是单调减函数,
上分别是单调减函数,
且x<1-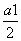 时y<1;x>1-
时y<1;x>1-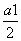 时y>1.
时y>1.
∵对任意的n∈N*,都有bn≤b4成立,
∴3<1-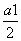 <4,
<4,
解得-6<a1<-4,即a1的取值范围为(-6,-4).

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
有编号为A1,A2,…,A10的10个零件,测量其直径(单位:cm),得到下面数据:
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.51 | 1.47 | 1.46 | 1.53 | 1.47 |
其中直径在区间[1.48,1.52]内的零件为一等品.
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件直径相等的概率.
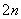 (n≥2),等比数列{bn}满足:bn+1bn-1=2bn(n≥2),则log2(a2+b2)=( )
(n≥2),等比数列{bn}满足:bn+1bn-1=2bn(n≥2),则log2(a2+b2)=( )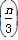 ,n∈N*,Sn为数列{an}的前n项和,则S3n的值为________.
,n∈N*,Sn为数列{an}的前n项和,则S3n的值为________. 与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )


 +y2=1的左、右焦点.
+y2=1的左、右焦点. =-
=- ,求点P的坐标;
,求点P的坐标;