题目内容
17．已知函数f（x）=$\left\{\begin{array}{l}{-丨x+1丨+3，x≤0}\\{f（x-4）+2，x＞0}\end{array}\right.$，若方程f（x）-3=kx有四个不同的实数解，则实数k的取值范围是（$\frac{4}{7}$，$\frac{2}{3}$）∪{$\frac{1}{4}$}．分析 化简f（x）-3=$\left\{\begin{array}{l}{-|x+1|，x≤0}\\{f（x-4）-1，x＞0}\end{array}\right.$，作函数f（x）-3与y=kx的图象，由几何意义求解即可．
解答 解：∵f（x）=$\left\{\begin{array}{l}{-丨x+1丨+3，x≤0}\\{f（x-4）+2，x＞0}\end{array}\right.$，
∴f（x）-3=$\left\{\begin{array}{l}{-|x+1|，x≤0}\\{f（x-4）-1，x＞0}\end{array}\right.$，
作函数f（x）-3与y=kx的图象如下，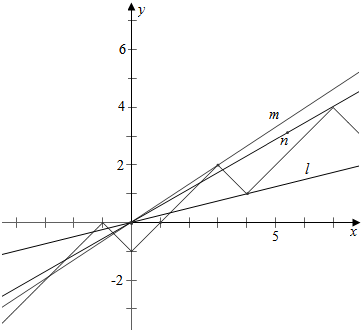
可知直线m的斜率km=$\frac{2-0}{3-0}$=$\frac{2}{3}$，直线n的斜率kn=$\frac{4}{7}$，
直线l的斜率kl=$\frac{1}{4}$；
故实数k的取值范围是（$\frac{4}{7}$，$\frac{2}{3}$）∪{$\frac{1}{4}$}．
故答案为：（$\frac{4}{7}$，$\frac{2}{3}$）∪{$\frac{1}{4}$}．
点评 本题考查了数形结合的思想应用，属于中档题．
练习册系列答案
相关题目
7．如果在区间[1，3]上，函数f（x）=x2+px+q与g（x）=2x+$\frac{1}{{x}^{2}}$在同一点取得相同的最小值，那么下列说法不对的是（ ）
| A． | f（x）≥3（x∈[1，2]） | B． | f（x）≤4（x∈[1，2]） | ||
| C． | f（x）在x∈[1，2]上单调递增 | D． | f（x）在x∈[1，2]上是减函数 |