Question

12．在凸四边形ABCD中，AB=2，BC=3，CD=5，AD=4，求凸四边形面积最大值．

Answer 1

分析 连接AC，如图所示，在三角形ABC和三角形ADC中，分别利用余弦定理列出关系式，整理得到15cosD-8cosB=7；利用三角形面积公式表示出S，整理得到8sinB+15sinD=2S，两关系式联立表示出S²，利用余弦函数的值域确定出S最大值即可．

解答 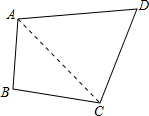解：连接AC，设AC=x，
在△ABC中，由余弦定理得：x²=2²+4²-2×2×4cosB=20-16cosB①，
在△ADC中，由余弦定理得：x²=3²+5²-2×3×5cosD=34-30cosD②，
由①②得：15cosD-8cosB=7③，
四边形ABCD面积S=$\frac{1}{2}$×2×4sinB+$\frac{1}{2}$×3×5sinD=$\frac{1}{2}$（8sinB+15sinD），
整理得：8sinB+15sinD=2S④，
将③④两式平方相加得：64+225+240（sinBsinD-cosBcosD）=49+4S²，
整理得：S²=60-60cos（B+D），
∵-1≤cos（B+D）≤1，即0＜S²≤120，
当cos（B+D）=-1，即B+D=π时，（S²）_max=120，即S_max=2$\sqrt{30}$，
则S的最大值为2$\sqrt{30}$．

点评 此题考查了余弦定理，余弦函数的值域，以及三角形面积公式，熟练掌握余弦定理是解本题的关键．