题目内容
7.若半径为2 的球O中有一内接圆柱,当圆柱的侧面积为8π时,圆柱的体积为4$\sqrt{2}π$.分析 设半径为R=2 的球O中的内接圆柱的高为h,底面半径为r,由圆柱的侧面积为8π,列出方程组,求出r=$\sqrt{2}$,h=2$\sqrt{2}$,由此能求出圆柱的体积.
解答 解: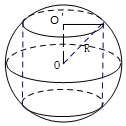 如图,设半径为R=2 的球O中的内接圆柱的高为h,底面半径为r,
如图,设半径为R=2 的球O中的内接圆柱的高为h,底面半径为r,
∵圆柱的侧面积为8π,
∴$\left\{\begin{array}{l}{2πrh=8π}\\{{r}^{2}+(\frac{1}{2}h)^{2}=4}\end{array}\right.$,解得r=$\sqrt{2}$,h=2$\sqrt{2}$,
∴圆柱的体积V=πr2h=$π×(\sqrt{2})^{2}×2\sqrt{2}$=4$\sqrt{2}π$.
故答案为:4$\sqrt{2}π$.
点评 本题考查圆柱的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
20.若x、y满足约束条件$\left\{\begin{array}{l}3x+y-6≤0\\ x+y≥2\\ y≤2\end{array}\right.$,则x2+y2的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 5 |
18. 如图是正方体的平面展开图.关于这个正方体,有以下判断:
如图是正方体的平面展开图.关于这个正方体,有以下判断:
①ED与NF所成的角为60°
②CN∥平面AFB
③BM∥DE
④平面BDE∥平面NCF
其中正确判断的序号是( )
 如图是正方体的平面展开图.关于这个正方体,有以下判断:
如图是正方体的平面展开图.关于这个正方体,有以下判断:①ED与NF所成的角为60°
②CN∥平面AFB
③BM∥DE
④平面BDE∥平面NCF
其中正确判断的序号是( )
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②③④ |
15.下列各组数,可以是钝角三角形的长的是( )
| A. | 6,7,8 | B. | 7,8,10 | C. | 2,6,7 | D. | 5,12,13 |
12.某大学中文系一、二、三、四年级的学生数之比为5:2:3:4,要用分层抽样的方法从该系所有本科生中抽取一个容量为280的样本,则应抽取二年级的学生为( )
| A. | 40人 | B. | 60人 | C. | 80人 | D. | 20人 |
17. 面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.
 面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.频率分布表
| 分组 | 频数 | 频率 |
| [100,150) | 1 | 0.05 |
| [150,200) | 3 | 0.15 |
| [200,250) | x | 0.1 |
| [250,300) | 6 | 0.3 |
| [300,350) | 4 | 0.2 |
| [350,400) | 3 | y |
| [400,450] | 1 | 0.05 |
| 合计 | N | 1 |
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.