题目内容
已知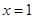 是函数
是函数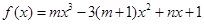 的一个极值点,其中
的一个极值点,其中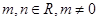
(1)求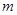 与
与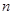 的关系式;
的关系式;
(2)求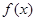 的单调区间;
的单调区间;
(3)设函数函数g(x)=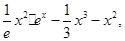
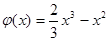 ;试比较g(x)与
;试比较g(x)与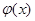 的大小。
的大小。
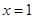 是函数
是函数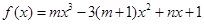 的一个极值点,其中
的一个极值点,其中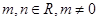
(1)求
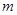 与
与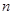 的关系式;
的关系式;(2)求
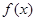 的单调区间;
的单调区间;(3)设函数函数g(x)=
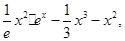
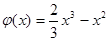 ;试比较g(x)与
;试比较g(x)与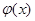 的大小。
的大小。(1) 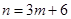
(2) 当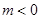 时,
时,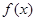 在
在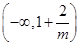 单调递减,在
单调递减,在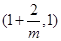 单调递增,在
单调递增,在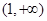 上单调递减.同理可得:当
上单调递减.同理可得:当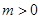 时,
时,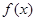 在
在 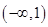 单调递增,在
单调递增,在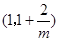 单调递减,在
单调递减,在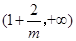 上单调递增
上单调递增
(3)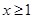 时 ,g(x)
时 ,g(x)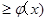
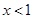 时, g(x)
时, g(x)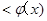
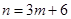
(2) 当
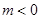 时,
时,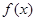 在
在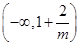 单调递减,在
单调递减,在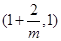 单调递增,在
单调递增,在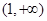 上单调递减.同理可得:当
上单调递减.同理可得:当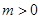 时,
时,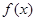 在
在 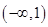 单调递增,在
单调递增,在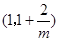 单调递减,在
单调递减,在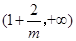 上单调递增
上单调递增(3)
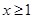 时 ,g(x)
时 ,g(x)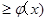
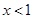 时, g(x)
时, g(x)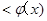
试题分析:解(I)
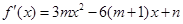 因为
因为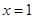 是函数
是函数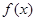 的一个极值点,所以
的一个极值点,所以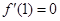 ,即
,即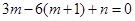 ,所以
,所以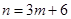 3分
3分(II)由(I)知,
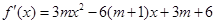 =
=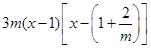 …5分
…5分当
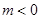 时,有
时,有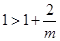 ,当
,当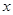 变化时,
变化时,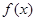 与
与 的变化如下表:
的变化如下表: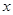 | 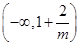 | 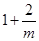 | 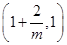 | 1 | 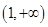 |
 | 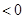 | 0 | 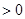 | 0 | 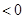 |
| | | | | | |
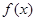 | 调调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
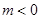 时,
时,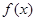 在
在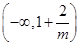 单调递减,在
单调递减,在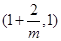 单调递增,在
单调递增,在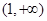 上单调递减.同理可得:当
上单调递减.同理可得:当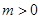 时,
时,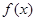 在
在 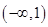 单调递增,在
单调递增,在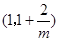 单调递减,在
单调递减,在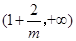 上单调递增. 9分
上单调递增. 9分(III)设函数h(x)=
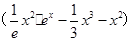 -
-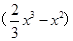 =
=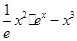 =
=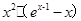
由
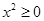 ,且
,且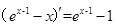 ,故
,故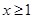 ,
,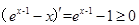
令
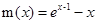 所以m(x)在
所以m(x)在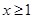 为增函数,故
为增函数,故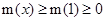
所以h(x)在
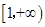 ,h(x)
,h(x)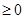 ,故g(x)
,故g(x)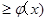
当
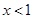 ,
,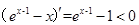
令
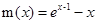 所以m(x)在
所以m(x)在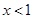 为减函数,故
为减函数,故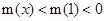
所以h(x)在
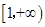 ,h(x)
,h(x)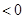 ,故g(x)
,故g(x)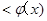
综上
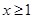 时 ,g(x)
时 ,g(x)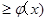 14分
14分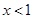 时, g(x)
时, g(x)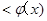
点评:解决的关键是利用导数的符号与函数单调性的关系来确定单调性,以及极值问题,并利用单调性来比较大小,属于中档题。

练习册系列答案
相关题目
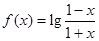 .
.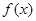 的定义域;
的定义域;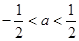 ,试比较
,试比较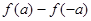 与
与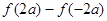 的大小.
的大小.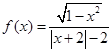 (2)
(2)
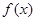 的定义域为
的定义域为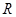 ,若存在常数
,若存在常数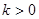 ,使
,使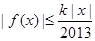 对一切实数
对一切实数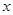 均成立
均成立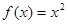 ;②
;②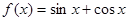 ;③
;③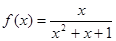 ;④
;④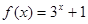 .
.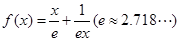 .
.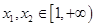 ,
,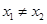 ,求证:
,求证: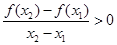 ;
;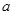 满足
满足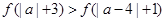 .试求
.试求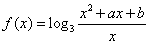 ,
,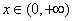 ,是否存在实数
,是否存在实数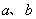 ,使
,使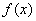 同时满足下列两个条件:(1)
同时满足下列两个条件:(1)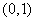 上是减函数,在
上是减函数,在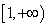 上是增函数;(2)
上是增函数;(2) ,若存在,求出
,若存在,求出 的单调增区间与值域相同,则实数
的单调增区间与值域相同,则实数 的取
的取
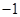
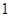
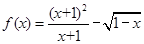 的定义域;(6分)
的定义域;(6分)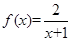 在
在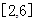 上的值域.(6分)
上的值域.(6分)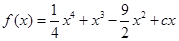 有三个极值点。
有三个极值点。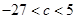 ;
;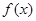 在区间
在区间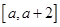 上单调递减,求
上单调递减,求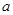 的取值范围。
的取值范围。