题目内容
(1)求函数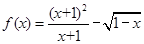 的定义域;(6分)
的定义域;(6分)
(2)求函数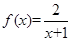 在
在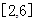 上的值域.(6分)
上的值域.(6分)
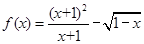 的定义域;(6分)
的定义域;(6分)(2)求函数
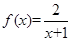 在
在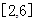 上的值域.(6分)
上的值域.(6分)(1) ;(2)
;(2) 。
。
 ;(2)
;(2) 。
。试题分析:(1)由
 ,所以函数
,所以函数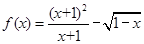 的定义域为
的定义域为 。
。(2)因为函数
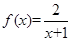 在
在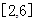 上单调递减,所以
上单调递减,所以 ,所以函数
,所以函数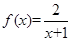 在
在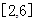 上的值域为
上的值域为 。
。点评:本题直接考查函数的定义域和值域的求法,属于基础题型。在求函数的定义域和值域时,最后结果一定要写成集合或区间的形式。

练习册系列答案
相关题目
题目内容
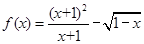 的定义域;(6分)
的定义域;(6分)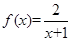 在
在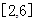 上的值域.(6分)
上的值域.(6分) ;(2)
;(2) 。
。 ,所以函数
,所以函数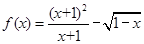 的定义域为
的定义域为 。
。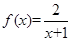 在
在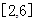 上单调递减,所以
上单调递减,所以 ,所以函数
,所以函数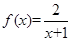 在
在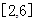 上的值域为
上的值域为 。
。