题目内容
函数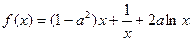 .
.
(Ⅰ)当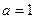 时,求
时,求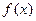 的最小值;
的最小值;
(Ⅱ)当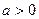 时,求
时,求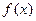 的单调区间.
的单调区间.
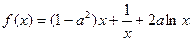 .
.(Ⅰ)当
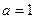 时,求
时,求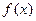 的最小值;
的最小值; (Ⅱ)当
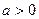 时,求
时,求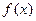 的单调区间.
的单调区间.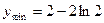 ,单减区间是
,单减区间是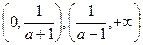 ,
,单增区间是
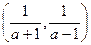 .
.解:(1)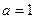 时,
时,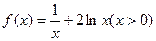 ,
,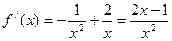
令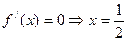 ,当
,当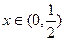 时,
时,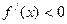 ;当
;当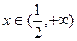 时,
时,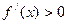 ∴
∴
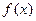 有极小值
有极小值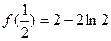 ,即
,即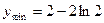 .
.
(2)定义域是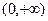 ,
,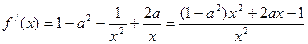
∵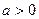 ,于是有
,于是有
① 当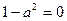 ,即
,即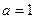 时,
时,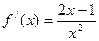
∴单减区间是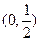 ,单增区间为
,单增区间为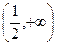 .
.
② 当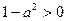 即
即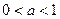 时,
时,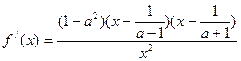 由数轴标根法并结合定义域
由数轴标根法并结合定义域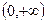 可知:单减区间
可知:单减区间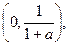 单增区间为
单增区间为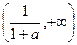 .
.
③ 当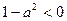 时,即
时,即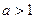 时,
时,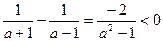 即
即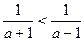
由数轴标根法并结合定义域可知:单减区间是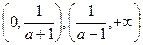 ,
,
单增区间是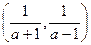 .
.
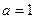 时,
时,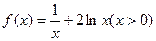 ,
,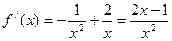
令
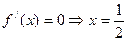 ,当
,当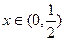 时,
时,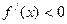 ;当
;当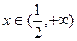 时,
时,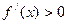 ∴
∴
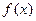 有极小值
有极小值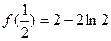 ,即
,即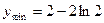 .
.(2)定义域是
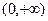 ,
,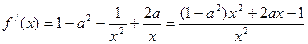
∵
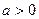 ,于是有
,于是有 ① 当
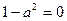 ,即
,即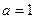 时,
时,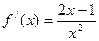
∴单减区间是
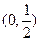 ,单增区间为
,单增区间为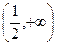 .
.② 当
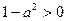 即
即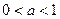 时,
时,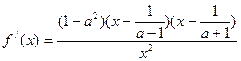 由数轴标根法并结合定义域
由数轴标根法并结合定义域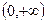 可知:单减区间
可知:单减区间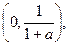 单增区间为
单增区间为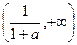 .
.③ 当
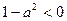 时,即
时,即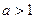 时,
时,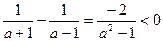 即
即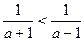
由数轴标根法并结合定义域可知:单减区间是
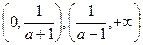 ,
,单增区间是
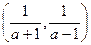 .
.
练习册系列答案
相关题目
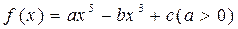 .
. 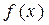 在
在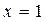 和
和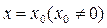 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,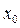 及实数
及实数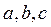 的值;
的值;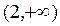 上单调递增且
上单调递增且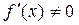 ,求
,求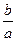 的最大值.
的最大值. 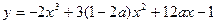 在x=α处取得极小值,在x=β处取得极大值,且α2=β
在x=α处取得极小值,在x=β处取得极大值,且α2=β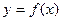 在
在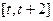 上的最大值g(t)。
上的最大值g(t)。  题满分 13分)设函数
题满分 13分)设函数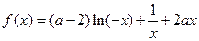 (
(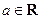 ).
).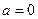 时,求
时,求 的极值;
的极值;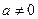 时,求
时,求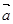 =(1,1),设f(x)=
=(1,1),设f(x)=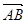 ·
·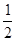 x
x ≤f(x
≤f(x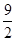 m-3都恒成立,求实数m的取值范围.
m-3都恒成立,求实数m的取值范围.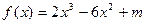 (m为常数)在
(m为常数)在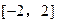 上有最大值3,那么此函数在
上有最大值3,那么此函数在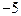
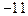
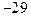
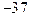
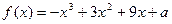 ,若
,若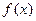 在区间[-2,2]上的最大值为20.
在区间[-2,2]上的最大值为20.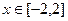 时,
时,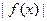 ≤m,(m>0)恒成立.求m的取值范围.
≤m,(m>0)恒成立.求m的取值范围.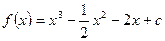 ,若对任意
,若对任意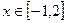 都有
都有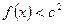 ,则
,则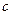 的取值范围是 .
的取值范围是 .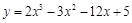 在区间[0,3]上的最大值与最小值分别是( )
在区间[0,3]上的最大值与最小值分别是( )