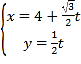题目内容
【题目】已知抛物线
和圆
，抛物线
的焦点为
.
（1）求
的圆心到的准线的距离；
（2）若点
在抛物线上，且满足
， 过点作圆的两条切线，记切点为
，求四边形
的面积的取值范围；
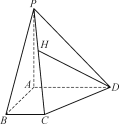
（3）如图，若直线
与抛物线和圆依次交于
四点，证明:
的充要条件是“直线的方程为
”
【答案】（1）4；（2）
；（3）见解析
【解析】
（1）分别求出圆心和准线方程即可得解；
（2）根据条件可表示出四边形
的面积
，利用函数的单调性即可得解；
（3）充分性：令直线
的方程为
，分别求出
、
、
、
四点坐标后即可证明
；必要性：设的方程为
，
，
，
，
，由可得
，即可得出
与
的关系，进而可得出直线的方程为.
（1）由
可得:
，
的圆心与
的焦点
重合，
的圆心
到的准线
的距离为
.
（2）四边形的面积为:
，
当
时，四边形的面积的取值范围为.
（2）证明(充分性) :若直线的方程为，将分别代入
得
，
，
，
.
，.
(必要性) :若，则线段
与线段
的中点重合，
设的方程为，，，，，
则，将代入得
，
，
即
，
同理可得，
，
即
或
，
而当时，将其代入得
不可能成立； .
当时，由
得：
，
，
将
代入得
，
，
，
，
，
或
（舍去）
直线的方程为.
的充要条件是“直线的方程为”.
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
【题目】某汽车公司生产新能源汽车，2019年3-9月份销售量（单位：万辆）数据如下表所示：
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
销售量 （万辆） | 3.008 | 2.401 | 2.189 | 2.656 | 1.665 | 1.672 | 1.368 |
（1）某企业响应国家号召，购买了6辆该公司生产的新能源汽车，其中四月份生产的4辆，五月份生产的2辆，6辆汽车随机地分配给A，B两个部门使用，其中A部门用车4辆，B部门用车2辆.现了解该汽车公司今年四月份生产的所有新能源汽车均存在安全隐患，需要召回.求该企业B部门2辆车中至多有1辆车被召回的概率；
（2）经分析可知，上述数据近似分布在一条直线附近.设
关于
的线性回归方程为
，根据表中数据可计算出
，试求出
的值，并估计该厂10月份的销售量.
