题目内容
【题目】数列![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和(
项和(![]() ).
).
(1)设数列![]() 是首项和公比都为
是首项和公比都为![]() 的等比数列,且数列
的等比数列,且数列![]() 也是等比数列,求
也是等比数列,求![]() 的值;
的值;
(2)设![]() ,若
,若![]() 且
且![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ),若存在整数
),若存在整数![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() 成立,求
成立,求![]() 的所有可能值.
的所有可能值.
【答案】(1)![]()
(2)![]()
(3)![]() 和
和![]()
【解析】
(1)直接利用等比数列的定义和等比中项的应用求出结果.
(2)利用累加法和恒成立问题的应用和赋值法的应用求出结果.
(3)利用存在性问题的应用和赋值法的应用求出结果.
解:(1) 由条件得![]() ,
,![]() ,即
,即![]() ,
,
则![]() ,
,![]() ,设等比数列
,设等比数列![]() 的公比为
的公比为![]() ,
,
则![]() ,又
,又![]() ,则
,则![]() .
.
当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
则![]() 满足题意,
满足题意,
故所求的![]() 的值为
的值为![]() .
.
(2)当![]() 时,
时,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
以上![]() 个式子相加得,
个式子相加得,![]() ,
,
又![]() ,则
,则![]() ,
,
即![]() . 由
. 由![]() 知数列
知数列![]() 是递增数列,
是递增数列,
又![]() ,要使得
,要使得![]() 对
对![]() 恒成立,
恒成立,
则只需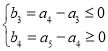 ,即
,即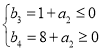 ,则
,则![]() .
.
(3) 由条件得数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,
为公差的等差数列,
则![]() ,
,![]() ,
,
则![]() .
.
则![]() ,
,
当![]() 时,
时,![]() ,
,
即![]() 时,
时,![]() ,
,
则当![]() 时,
时,![]() 与
与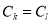 矛盾.
矛盾.
又![]() ,即
,即![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,
又![]() ,
,
即当![]() ,
,![]() 时,
时,![]() ,与
,与![]() 矛盾.
矛盾.
又![]() ,则
,则![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() .
.
综上得![]() 的所有可能值为
的所有可能值为![]() 和
和![]() .
.

练习册系列答案
相关题目