题目内容
【题目】已知椭圆![]() (
(![]() )的右焦点为F,左顶点为A,离心率
)的右焦点为F,左顶点为A,离心率![]() ,且经过圆O:
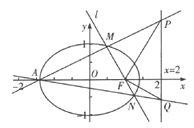
,且经过圆O:![]() 的圆心.过点F作不与坐标轴重合的直线
的圆心.过点F作不与坐标轴重合的直线![]() 和该椭圆交于MN两点,且直线
和该椭圆交于MN两点,且直线![]()
![]() 分别与直线
分别与直线![]() 交于PQ两点.
交于PQ两点.
(1)求椭圆的方程;
(2)证明:![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
根据条件椭圆过点![]() ,即
,即![]() ,由
,由![]() 以及
以及![]() ,可求椭圆方程.
,可求椭圆方程.
(2)设![]() ,
,![]() ,根据点共线求出点
,根据点共线求出点![]() 坐标,设直线的方程
坐标,设直线的方程![]() ,代入椭圆方程,利用韦达定理及直线的斜率公式即可得到
,代入椭圆方程,利用韦达定理及直线的斜率公式即可得到![]() ,即证明结论成立.
,即证明结论成立.
(1)由题意知,圆O:![]() 的圆心为
的圆心为![]()
.∵椭圆![]() (
(![]() )过圆O:
)过圆O:![]() 的圆心
的圆心![]() ,
,
∴![]() .又
.又![]() ,
,![]() ,∴
,∴![]()
.∴所求椭圆的方程为![]() .
.
(2)设![]() ,
,![]() ,可设直线l的方程为
,可设直线l的方程为![]() .
.
联立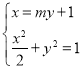 ,可得
,可得![]() .
.
∴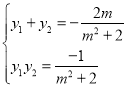
.根据AMP三点共线可得![]() .
.
∴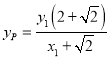 .同理可得
.同理可得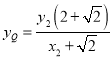
.∴PQ的坐标分别为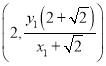 ,
,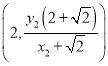 .
.
设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则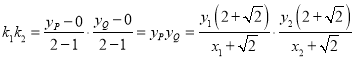
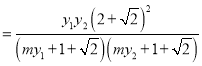
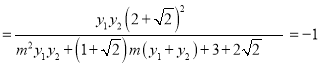
∴![]() . ∴
. ∴![]() 为直角三角形.
为直角三角形.

练习册系列答案
相关题目