题目内容
【题目】已知直三棱柱![]() 中,
中,![]() ,且
,且![]() ,点D,E,F分别为
,点D,E,F分别为![]() ,
,![]() ,BC中点.
,BC中点.
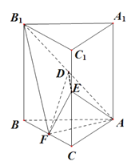
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积
的体积
【答案】(1)见解析(2)![]()
【解析】
(1)连接![]() ,
,![]() ,在直三棱柱
,在直三棱柱![]() 中,易得D是
中,易得D是![]() 中点,又F是BC中点,可得
中点,又F是BC中点,可得![]() ,再由线面平行的判定定理证明.
,再由线面平行的判定定理证明.
(2)在![]() 为等腰直角三角形中,根据F是BC中点,得到
为等腰直角三角形中,根据F是BC中点,得到![]() ,由直三棱柱得到
,由直三棱柱得到![]() ,从而
,从而![]() 平面
平面![]() ,可得
,可得![]() .在面
.在面![]() 中,由平面几何知识得到
中,由平面几何知识得到![]() ,证得
,证得![]() 平面
平面![]() ,所以EF为高,再求得
,所以EF为高,再求得![]() ,代入体积公式求解.
,代入体积公式求解.
(1)如图所示:

连接![]() ,
,![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,
侧面![]() 是平行四边形,”
是平行四边形,”
∵平行四边形对角线互相平分,D是![]() 中点,
中点,
∴D是![]() 中点,
中点,
又F是BC中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,
∵F是BC中点,∴![]() ,
,
直三棱柱![]() 中,
中,![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
∴![]() ,∵
,∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又∵![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() 平面ADF.
平面ADF.
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】![]() 年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小区年龄处于
年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小区年龄处于![]() 岁的人中随机地抽取
岁的人中随机地抽取![]() 人,进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
人,进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
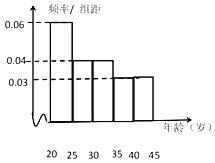
组数 | 分组 | “环保族”人数 | 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该区间的中点值代替,结果按四舍五入保留整数);
人年龄的平均值(同一组数据用该区间的中点值代替,结果按四舍五入保留整数);
(3)从年龄段在![]() 的“环保族”中采取分层抽样的方法抽取
的“环保族”中采取分层抽样的方法抽取![]() 人进行专访,并在这
人进行专访,并在这![]() 人中选取
人中选取![]() 人作为记录员,求选取的
人作为记录员,求选取的![]() 名记录员中至少有一人年龄在
名记录员中至少有一人年龄在![]() 中的概率.
中的概率.