题目内容
1.已知函数f(x)=a(x-a)(x+a+3),g(x)=2x-2,若对任意x∈R,总有f(x)<0或g(x)<0成立,则实数a的取值范围是( )| A. | (-∞,-4) | B. | [-4,0) | C. | (-4,0) | D. | (-4,+∞) |
分析 由题意可知x<1时,g(x)<0成立,进而得到a(x+a)(x-2a+1)<0对x≥1均成立,得到a满足的条件$\left\{\begin{array}{l}{a<0}\\{a<1}\\{-a-3<1}\end{array}\right.$,求解不等式组可得答案.
解答 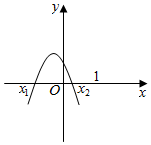 解:由g(x)=2x-2<0,得x<1,故对x≥1时,g(x)<0不成立,
解:由g(x)=2x-2<0,得x<1,故对x≥1时,g(x)<0不成立,
从而对任意x≥1,f(x)<0恒成立,
由于a(x-a)(x+a+3)<0对任意x≥1恒成立,如图所示,
则必满足$\left\{\begin{array}{l}{a<0}\\{a<1}\\{-a-3<1}\end{array}\right.$,
解得-4<a<0.
则实数a的取值范围是(-4,0).
故选:C.
点评 本题考查了函数的值,考查了不等式的解法,体现了恒成立思想的应用,属于中档题.

练习册系列答案
相关题目
12.已知命题p:-1≤x≤5,命题q:(x-5)(x+1)<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知直线a,b,c和平面α,给出下列两个命题:
命题p:若a∥α,b∥α,则a∥b;
命题q:若a∥b,b∥c,则a∥c.
那么下列判断正确的是( )
命题p:若a∥α,b∥α,则a∥b;
命题q:若a∥b,b∥c,则a∥c.
那么下列判断正确的是( )
| A. | p为真命题 | B. | q为假命题 | C. | (¬p)∧q为真命题 | D. | (¬p)∨q为假命题 |
10.已知空间两点A(1,2,z),B(2,-1,1)之间的距离为$\sqrt{11}$,则z=( )
| A. | 2 | B. | 0或2 | C. | 0 | D. | 2或1 |
11.下列各式错误的是( )
| A. | 30.8>30.7 | B. | log0.60.4>log0.60.5 | ||
| C. | log0.750.34>logπ3.14 | D. | 0.75-0.3<0.750.1 |