题目内容
方程x2sinα-y2cosα=1(0＜α＜π)表示焦点在y轴上的椭圆，求α的取值范围.
解：∵x2sinα-y2cosα=1,
∴
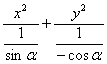=1.
∵焦点在y轴上，
∴a2=
,b2=
.
∴
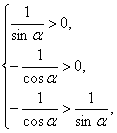
即
∵0＜α＜π,∴sinα＞0成立.
由
得tanα＜-1,∴α∈(
,
).
练习册系列答案
相关题目
方程
+
=1所表示的曲线是（ ）
| x2 |
| sin(192010)0 |
| y2 |
| cos(192010)0 |
| A、双曲线 |
| B、焦点在x轴上的椭圆 |
| C、焦点在y轴上的椭圆 |
| D、以上答案都不对 |
设θ是三角形的一个内角，且sinθ+cosθ=
，则方程x2sinθ-y2cosθ=1表示的曲线是（ ）
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在x轴上的椭圆 |
| C、焦点在y轴上的双曲线 |
| D、焦点在y轴上的椭圆 |