题目内容
已知关于x的方程lnx-ax=0恰有一个实根,则实数a的取值范围分析:先构造函数y=lnx-ax,借助于导数,进行分类讨论,可知当a≤0时,(0,1]之间必有一个实根;a=
时,也恰有一个实根.
| 1 |
| e |
解答:解:设y=lnx-ax,则y'=
-a=0,x=
,y“=-
<0
当a≤0,y'>0,最多有一个实根,因 y(0-)<0,y(1)≥0,所以(0,1]之间必有一个实根
a>0,x=
,y=-lna-1为极大值,此极大值若为0的话,则有一个实根,此时a=
此极大值若大于0的话,会有两个实根,此极大值若小于0的话,则无实根.
因此a的取值范围为:(-∞,0]∪{
},
故答案为(-∞,0]∪{
}
| 1 |
| x |
| 1 |
| a |
| 1 |
| x2 |
当a≤0,y'>0,最多有一个实根,因 y(0-)<0,y(1)≥0,所以(0,1]之间必有一个实根
a>0,x=
| 1 |
| a |
| 1 |
| e |
因此a的取值范围为:(-∞,0]∪{
| 1 |
| e |
故答案为(-∞,0]∪{
| 1 |
| e |
点评:本题利用导数解决方程根的个数问题,有一定难度,应注意细细体会.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
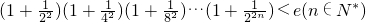 .
. .
.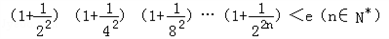 .
.