题目内容
已知函数fn(x)=1+x+x2+…+xn(n∈N*).
(1)当n=1,2,3时,分别求函数fn(x)的单调区间;
(2)当n=2时,关于x的方程ln(x+1)=-
x+m+f(x)-1在区间[0,2]上恰有两个不同的实数根,求实数m的取值范围;
(3)求证:对任意的正整数n,不等式ln
<
都成立.
(1)当n=1,2,3时,分别求函数fn(x)的单调区间;
(2)当n=2时,关于x的方程ln(x+1)=-
| 5 |
| 2 |
(3)求证:对任意的正整数n,不等式ln
| n+1 |
| n |
| n+1 |
| n2 |
分析:(1)当n=1时直接利用一次函数的单调性即可,当n=2时借助于二次函数的单调性;当n=3时,求出其导函数即可求出函数fn(x)的单调区间;
(2)先把问题转化为h(x)=ln(x+1)-x2+
x-m在区间[0,2]上与x轴恰有两个不同的交点;求出其导函数,得到其单调性,根据其端点值满足的条件即可求出实数m的取值范围;
(3)先令g(x)=ln(x+1)-x2-x,根据其导函数得到其在定义域上的最大值,再取x=
,即可证明结论成立.
(2)先把问题转化为h(x)=ln(x+1)-x2+
| 3 |
| 2 |
(3)先令g(x)=ln(x+1)-x2-x,根据其导函数得到其在定义域上的最大值,再取x=
| 1 |
| n |
解答:解:(1)当n=1时,f(x)=1+x在区间(-∞,+∞)上单调递增;
当n=2时,f(x)=1+x+x2在区间(-∞,-
)上单调递减,在区间(-
,+∞)上单调递增:
当n=3时,f(x)=1+x+x2+x3,导函数f''(x)=1+2x+3x2>0对x∈R成立,f(x)=1+x+x2+x3在区间(-∞,+∞)上单调递增.
(2)由ln(x+1)=-
+m+f(x)-1得:h(x)=ln(x+1)-x2+
x-m在区间[0,2]上与x轴恰有两个不同的交点
h/(x)=
-2x+
=
当x∈(0,1)时,h′(x)>0,则h(x)在区间(0,1)上单调递增;
当x∈(1,2)时,h′(x)<0,则h(x)在区间(1,2)上单调递减;
由题意得:
则ln3-1≤m<ln2+
(3)令g(x)=ln(x+1)-x2-x,它的定义域为{x|x>-1}.
∴g/(x)=
当x∈(-1,0)时,g′(x)>0,则g(x)在区间(-1,0)上单调递增;
当x∈(0,+∞)时,g′(x)<0,则g(x)在区间(0,+∞)上单调递减;
∴g(0)为g(x)在(-1,+∞)上的最大值
∴g(x)≤g(0)即ln(x+1)-x2-x≤0(当且仅当x=0时,等号成立)
∴对任意n∈N*,取x=
,则不等式ln
<
都成立.
当n=2时,f(x)=1+x+x2在区间(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
当n=3时,f(x)=1+x+x2+x3,导函数f''(x)=1+2x+3x2>0对x∈R成立,f(x)=1+x+x2+x3在区间(-∞,+∞)上单调递增.
(2)由ln(x+1)=-
| 5 |
| 2 |
| 3 |
| 2 |
h/(x)=
| 1 |
| x+1 |
| 3 |
| 2 |
| -(4x+5)(x-1) |
| 2(x+1) |
当x∈(0,1)时,h′(x)>0,则h(x)在区间(0,1)上单调递增;
当x∈(1,2)时,h′(x)<0,则h(x)在区间(1,2)上单调递减;
由题意得:
|
| 1 |
| 2 |
(3)令g(x)=ln(x+1)-x2-x,它的定义域为{x|x>-1}.
∴g/(x)=
| -x(2x+3) |
| x+1 |
当x∈(-1,0)时,g′(x)>0,则g(x)在区间(-1,0)上单调递增;
当x∈(0,+∞)时,g′(x)<0,则g(x)在区间(0,+∞)上单调递减;
∴g(0)为g(x)在(-1,+∞)上的最大值
∴g(x)≤g(0)即ln(x+1)-x2-x≤0(当且仅当x=0时,等号成立)
∴对任意n∈N*,取x=
| 1 |
| n |
| n+1 |
| n |
| n+1 |
| n2 |
点评:本题主要考查了利用导数求闭区间上函数的最值以及研究函数的单调性,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.

练习册系列答案
相关题目
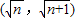 上零点的个数,并给予证明.
上零点的个数,并给予证明.