题目内容
已知函数f(x)=ax2+bx+c和函数g(x)=ln(1+x2)+ax(a<0).
(Ⅰ)求函数g(x)的单调区间;
(Ⅱ)已知关于x的方程f(x)=x没有实数根,求证方程f(f(x))=x也没有实数根;
(Ⅲ)证明: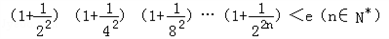 .
.
(Ⅰ)求函数g(x)的单调区间;
(Ⅱ)已知关于x的方程f(x)=x没有实数根,求证方程f(f(x))=x也没有实数根;
(Ⅲ)证明:
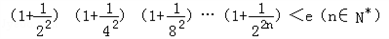 .
.(Ⅰ)解: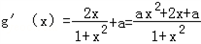
①当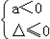 ,即a≤﹣1时,g′(x)≤0对x∈R恒成立,∴g(x)在(﹣∞,+∞)上单调递减;
,即a≤﹣1时,g′(x)≤0对x∈R恒成立,∴g(x)在(﹣∞,+∞)上单调递减;
②当﹣1<a<0时,令g′(x)>0,则ax2+2x+a>0
∴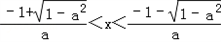 ,
,
令g′(x)<0,则ax2+2x+a<0
∴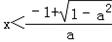 或
或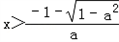 ,
,
∴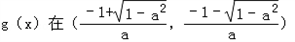 上单调递增,在
上单调递增,在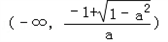 和
和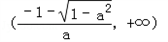 上单调递减;
上单调递减;
综上所述,当a≤﹣1时,g(x)在(﹣∞,+∞)上单调递减,
当﹣1<a<0时,g(x)在 上单调递增,
上单调递增,
在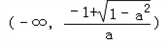 和
和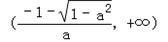 上单调递减.
上单调递减.
(Ⅱ)证明:∵关于x的方程f(x)=x没有实数根
∴ax2+bx+c=x没有实数根
∴ax2+(b﹣1)x+c=0没有实数根
∴△=(b﹣1)2﹣4ac<0
∵f(f(x))=x
∴a(ax2+bx+c)2+b(ax2+bx+c)+c=x
∴[ax2+(b﹣1)x+c][a2x2+a(b+1)x+b+ac+1]=0
∵ax2+(b﹣1)x+c≠0
∴a2x2+a(b+1)x+b+ac+1=0
∵△=a2(b+1)2﹣4a2(b+ac+1)=a2[(b+1)2﹣4(b+ac+1)]=a2[(b﹣1)2﹣4ac﹣4]<0
∴a2x2+a(b+1)x+b+ac+1=0无实根
∴方程f(f(x))=x也没有实数根;
(Ⅲ)证明:由(Ⅰ)知,当a=﹣1时,g(x)在(﹣∞,+∞)上单调递减,
当x∈(0,+∞)时,由g(x)<g(0)=0
得:ln(1+x2)<x,
∴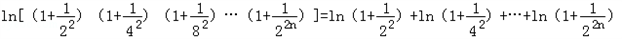
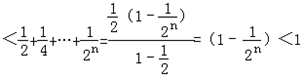 =lne,
=lne,
∴ e
e
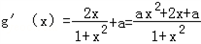
①当
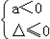 ,即a≤﹣1时,g′(x)≤0对x∈R恒成立,∴g(x)在(﹣∞,+∞)上单调递减;
,即a≤﹣1时,g′(x)≤0对x∈R恒成立,∴g(x)在(﹣∞,+∞)上单调递减;②当﹣1<a<0时,令g′(x)>0,则ax2+2x+a>0
∴
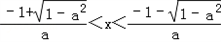 ,
,令g′(x)<0,则ax2+2x+a<0
∴
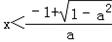 或
或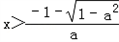 ,
,∴
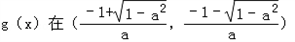 上单调递增,在
上单调递增,在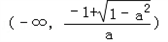 和
和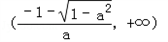 上单调递减;
上单调递减; 综上所述,当a≤﹣1时,g(x)在(﹣∞,+∞)上单调递减,
当﹣1<a<0时,g(x)在
 上单调递增,
上单调递增,在
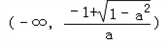 和
和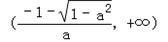 上单调递减.
上单调递减.(Ⅱ)证明:∵关于x的方程f(x)=x没有实数根
∴ax2+bx+c=x没有实数根
∴ax2+(b﹣1)x+c=0没有实数根
∴△=(b﹣1)2﹣4ac<0
∵f(f(x))=x
∴a(ax2+bx+c)2+b(ax2+bx+c)+c=x
∴[ax2+(b﹣1)x+c][a2x2+a(b+1)x+b+ac+1]=0
∵ax2+(b﹣1)x+c≠0
∴a2x2+a(b+1)x+b+ac+1=0
∵△=a2(b+1)2﹣4a2(b+ac+1)=a2[(b+1)2﹣4(b+ac+1)]=a2[(b﹣1)2﹣4ac﹣4]<0
∴a2x2+a(b+1)x+b+ac+1=0无实根
∴方程f(f(x))=x也没有实数根;
(Ⅲ)证明:由(Ⅰ)知,当a=﹣1时,g(x)在(﹣∞,+∞)上单调递减,
当x∈(0,+∞)时,由g(x)<g(0)=0
得:ln(1+x2)<x,
∴
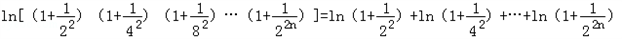
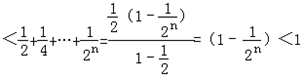 =lne,
=lne,∴
 e
e
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目