题目内容
已知函数f(x)=ax2+bx+c和函数g(x)=ln(1+x2)+ax(a<0).
(Ⅰ)求函数g(x)的单调区间;
(Ⅱ)已知关于x的方程f(x)=x没有实数根,求证方程f(f(x))=x也没有实数根;
(Ⅲ)证明: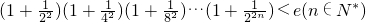 .
.
(Ⅰ)解:
①当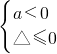 ,即a≤-1时,g′(x)≤0对x∈R恒成立,
,即a≤-1时,g′(x)≤0对x∈R恒成立,
∴g(x)在(-∞,+∞)上单调递减;
②当-1<a<0时,令g′(x)>0,则ax2+2x+a>0
∴ ,
,
令g′(x)<0,则ax2+2x+a<0
∴ 或
或 ,
,
∴ 上单调递增,在
上单调递增,在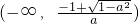 和
和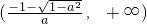 上单调递减;
上单调递减;
综上所述,当a≤-1时,g(x)在(-∞,+∞)上单调递减,
当-1<a<0时,g(x)在 上单调递增,在
上单调递增,在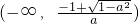 和
和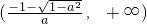 上单调递减.
上单调递减.
(Ⅱ)证明:∵关于x的方程f(x)=x没有实数根
∴ax2+bx+c=x没有实数根
∴ax2+(b-1)x+c=0没有实数根
∴△=(b-1)2-4ac<0
∵f(f(x))=x
∴a(ax2+bx+c)2+b(ax2+bx+c)+c=x
∴[ax2+(b-1)x+c][a2x2+a(b+1)x+b+ac+1]=0
∵ax2+(b-1)x+c≠0
∴a2x2+a(b+1)x+b+ac+1=0
∵△=a2(b+1)2-4a2(b+ac+1)=a2[(b+1)2-4(b+ac+1)]=a2[(b-1)2-4ac-4]<0
∴a2x2+a(b+1)x+b+ac+1=0无实根
∴方程f(f(x))=x也没有实数根;
(Ⅲ)证明:由(Ⅰ)知,当a=-1时,g(x)在(-∞,+∞)上单调递减,
当x∈(0,+∞)时,由g(x)<g(0)=0得:ln(1+x2)<x,
∴
 =lne,
=lne,
∴ e
e
分析:(Ⅰ)利用求导法则求出函数g(x)的导函数,把导函数解析式通分化简,分a小于等于-1,以及a大于-1小于0分别讨论导函数的正负,并利用二次函数的图象与性质,进而确定函数的单调性;
(Ⅱ)根据关于x的方程f(x)=x没有实数根,可得其判别式为0,再证明方程f(f(x))=x的判别式小于0即可;
(Ⅲ)a=-1时,g(x)在(-∞,+∞)上单调递减,可得a=-1时,函数为减函数,故当x>0时,g(x)<g(0),而g(0)=0,故g(x)<0,即ln(1+x2)<x,所证不等式左边取为e为底数的对数,利用对数的运算性质化简,并根据ln(1+x2)<x变形,再利用等比数列的前n项和公式化简,得出小于1,最后再根据对数的运算性质即可得证.
点评:本题重点考查用导函数的正负判断函数的单调性,考查二次函数的性质,不等式的证明,函数单调性的应用,以及对数的运算性质,考查等比数列的前n项和公式,综合性较强,难度较大.

①当
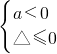 ,即a≤-1时,g′(x)≤0对x∈R恒成立,
,即a≤-1时,g′(x)≤0对x∈R恒成立,∴g(x)在(-∞,+∞)上单调递减;
②当-1<a<0时,令g′(x)>0,则ax2+2x+a>0
∴
 ,
,令g′(x)<0,则ax2+2x+a<0
∴
 或
或 ,
,∴
 上单调递增,在
上单调递增,在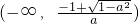 和
和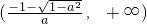 上单调递减;
上单调递减; 综上所述,当a≤-1时,g(x)在(-∞,+∞)上单调递减,
当-1<a<0时,g(x)在
 上单调递增,在
上单调递增,在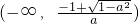 和
和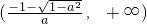 上单调递减.
上单调递减.(Ⅱ)证明:∵关于x的方程f(x)=x没有实数根
∴ax2+bx+c=x没有实数根
∴ax2+(b-1)x+c=0没有实数根
∴△=(b-1)2-4ac<0
∵f(f(x))=x
∴a(ax2+bx+c)2+b(ax2+bx+c)+c=x
∴[ax2+(b-1)x+c][a2x2+a(b+1)x+b+ac+1]=0
∵ax2+(b-1)x+c≠0
∴a2x2+a(b+1)x+b+ac+1=0
∵△=a2(b+1)2-4a2(b+ac+1)=a2[(b+1)2-4(b+ac+1)]=a2[(b-1)2-4ac-4]<0
∴a2x2+a(b+1)x+b+ac+1=0无实根
∴方程f(f(x))=x也没有实数根;
(Ⅲ)证明:由(Ⅰ)知,当a=-1时,g(x)在(-∞,+∞)上单调递减,
当x∈(0,+∞)时,由g(x)<g(0)=0得:ln(1+x2)<x,
∴

 =lne,
=lne,∴
 e
e分析:(Ⅰ)利用求导法则求出函数g(x)的导函数,把导函数解析式通分化简,分a小于等于-1,以及a大于-1小于0分别讨论导函数的正负,并利用二次函数的图象与性质,进而确定函数的单调性;
(Ⅱ)根据关于x的方程f(x)=x没有实数根,可得其判别式为0,再证明方程f(f(x))=x的判别式小于0即可;
(Ⅲ)a=-1时,g(x)在(-∞,+∞)上单调递减,可得a=-1时,函数为减函数,故当x>0时,g(x)<g(0),而g(0)=0,故g(x)<0,即ln(1+x2)<x,所证不等式左边取为e为底数的对数,利用对数的运算性质化简,并根据ln(1+x2)<x变形,再利用等比数列的前n项和公式化简,得出小于1,最后再根据对数的运算性质即可得证.
点评:本题重点考查用导函数的正负判断函数的单调性,考查二次函数的性质,不等式的证明,函数单调性的应用,以及对数的运算性质,考查等比数列的前n项和公式,综合性较强,难度较大.

练习册系列答案
相关题目