题目内容
2.已知函数f(x)=$\frac{x^3}{3}+\frac{1}{2}a{x^2}$+2bx+c(a,b,c∈R),函数f(x)的两个极值点分别在区间(0,1)与(1,2)内,则b-a+1的取值范围是(2,5).分析 由题意可知:f′(x)=x2+ax+2b,由x2+ax+2b=0的两个根分别在区间(0,1)与(1,2)内,$\left\{\begin{array}{l}{f′(0)=2b>0}\\{f′(1)=1+a+2b<0}\\{f′(2)=4+2a+2b>0}\end{array}\right.$,转化为在约束条件为$\left\{\begin{array}{l}{y>0}\\{1+x+2y<0}\\{2+x+y>0}\end{array}\right.$时,求z=y-x+1的取值范围,即可求得b-a+1的取值范围.
解答 解:由f(x)=$\frac{x^3}{3}+\frac{1}{2}a{x^2}$+2bx+c,求导f′(x)=x2+ax+2b,
f(x)的两个极值点分别在区间(0,1)与(1,2)内,求导f′(x)=x2+ax+2b,
由x2+ax+2b=0的两个根分别在区间(0,1)与(1,2)内,
即$\left\{\begin{array}{l}{f′(0)=2b>0}\\{f′(1)=1+a+2b<0}\\{f′(2)=4+2a+2b>0}\end{array}\right.$,令z=b-a+1,a=x,b=y,
∴转化为在约束条件为$\left\{\begin{array}{l}{y>0}\\{1+x+2y<0}\\{2+x+y>0}\end{array}\right.$时,求z=y-x+1的取值范围,可行域如下阴影(不包括边界),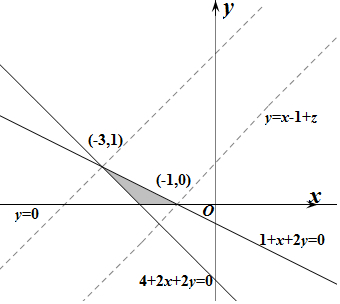
目标函数转化为y=x+z-1,由图可知,z在(-1,0)处取得最小值2,在(-3,1)处取得最大值5,
∴b-a+1的取值范围(2,5).
故答案为:(2,5).
点评 本题考查导数求导法则,导数极值的综合应用,考查平面线性规划的运用,考查学生的计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 200 | B. | 199 | C. | 299 | D. | 399 |
①5,9,100,107,111,121,180,195,200,265,
②7,34,61,88,115,142,169,196,223,250;
③30,57,84,111,138,165,192,219,246,270;
④11,38,65,92,119,146,173,200,227,254;
关于上述样本的下列结论中,正确的是( )
| A. | ②、④都可能为分层抽样 | B. | ①、③都不能为分层抽样 | ||
| C. | ①、④都可能为系统抽样 | D. | ②、③都不能为系统抽样 |
| A. | $-\frac{3}{5}$ | B. | $-\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
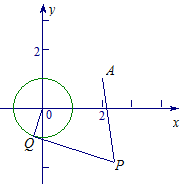 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.