题目内容
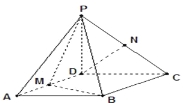
【题目】已知四棱锥![]() ,底面
,底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,又
的菱形,又![]() 底
底![]() ,且
,且![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.[
的距离.[
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)要证DN∥平面PMB,只要证DN∥MQ;(2)要证平面PMB⊥平面PAD,只要证MB⊥平面PAD;
(3)利用PD是三棱锥P-AMB的高PD=2,棱锥A-PMB的体积=棱锥P-AMB的体积,利用棱锥的体积公式解之
试题解析:(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 分别是棱
分别是棱![]() 中点,
中点,
所以![]() ,且
,且![]() ,于是
,于是![]() ,
,
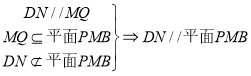 .
.
(2)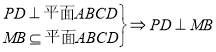 ,
,
又因为底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,且
的菱形,且![]() 为
为![]() 中点,所以
中点,所以![]() ,又
,又![]() ,
,
所以![]() .
.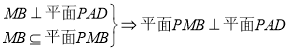 .
.
(3)因为![]() 是
是![]() 中点,所以点
中点,所以点![]() 与
与![]() 到平面
到平面![]() 等距离.过点
等距离.过点![]() 作
作![]() 于
于![]() ,由(2)由平面
,由(2)由平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故![]() 是点
是点![]() 到平面
到平面![]() 的距离
的距离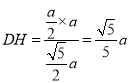 .
.
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在
处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在![]() 处的抽中率
处的抽中率![]() ,在
,在![]() 处的抽中率为
处的抽中率为![]() ,该同学选择现在
,该同学选择现在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.