题目内容
【题目】已知函数![]() 的一个零点为-2,当
的一个零点为-2,当![]() 时最大值为0.
时最大值为0.
(1)求![]() 的值;
的值;
(2)若对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先由零点的定义可得出关于![]() 的关系式,然后由二次函数的图像及其性质可得函数的最大值得出另一个关于
的关系式,然后由二次函数的图像及其性质可得函数的最大值得出另一个关于![]() 的关系式,最后联立方程即可得出
的关系式,最后联立方程即可得出![]() 的值;(2)首先将已知转化为
的值;(2)首先将已知转化为![]() 对
对![]() 恒成立,然后运用二次函数的图像及其性质可得出已知条件所满足的条件,进而得出所求的结果.
恒成立,然后运用二次函数的图像及其性质可得出已知条件所满足的条件,进而得出所求的结果.
试题解析:(1)![]() 的一个零点为-2,又当
的一个零点为-2,又当![]() 时最大值为0.即另一个零点在
时最大值为0.即另一个零点在![]() ,则
,则![]() ,即函数的两个零点分别为-2,4.
,即函数的两个零点分别为-2,4.![]()
或解:-2是零点,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() (舍去)
(舍去)
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,此时
,此时![]()
(2)由(1)知![]() ,
, ![]() ,即
,即![]() 对
对![]() 恒成立,则①
恒成立,则①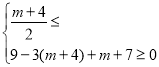 或②
或②![]()
![]()
解得①![]() 或 ②
或 ②![]() ,综合得m的取值范围为
,综合得m的取值范围为![]() .
.
(注:亦可分离变量![]() 对
对![]() 恒成立)
恒成立)

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目