题目内容
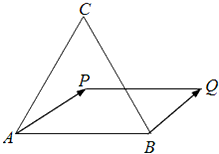 如图,正△ABC的边长为15,
如图,正△ABC的边长为15,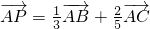 ,
,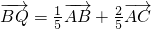 .
.
(1)求证:四边形APQB为梯形;
(2)求梯形APQB的面积.
解:(1)因
=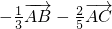
 =
=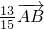 ,
,
故 ∥
∥ ,
,
且| |=13,|
|=13,| |=15,
|=15,
| |≠|
|≠| |,
|,
于是四边形APQB为梯形.
(2)设直线PQ交AC于点M,
则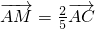 ,
,
故梯形APQB的高h为正△ABC的AB边上高的 ,
,
即 .
.
从而,梯形APQB的面积为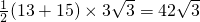 .
.
分析:(1)由已知中正△ABC的边长为15,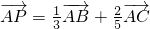 ,
,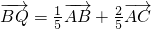 .根据向量加法的三角形法则,我们可得
.根据向量加法的三角形法则,我们可得 =
=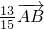 ,根据数乘向量的几何意义,我们可得
,根据数乘向量的几何意义,我们可得 ∥
∥ ,但|
,但| |≠|
|≠| |,进而根据梯形的判定定理得到四边形APQB为梯形;
|,进而根据梯形的判定定理得到四边形APQB为梯形;
(2)根据已知条件,结合(1)中的结论,我们可得| |=13,|
|=13,| |=15,梯形APQB的高h为正△ABC的AB边上高的
|=15,梯形APQB的高h为正△ABC的AB边上高的 ,代入梯形面积公式,即可求出梯形APQB的面积.
,代入梯形面积公式,即可求出梯形APQB的面积.
点评:本题考查的知识点是平面向量加法的三角形法则,数乘向量的几何意义,梯形面积公式,其中(1)的关键是根据向量加法的三角形法则,求出 =
=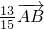 ,进而根据数乘向量的几何意义,分析PQ边与AB的关系,(2)的关键是根据已知求出梯形的上、下底边长及高的长度.
,进而根据数乘向量的几何意义,分析PQ边与AB的关系,(2)的关键是根据已知求出梯形的上、下底边长及高的长度.

=
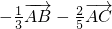
 =
=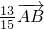 ,
,故
 ∥
∥ ,
,且|
 |=13,|
|=13,| |=15,
|=15,|
 |≠|
|≠| |,
|,于是四边形APQB为梯形.
(2)设直线PQ交AC于点M,
则
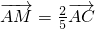 ,
,故梯形APQB的高h为正△ABC的AB边上高的
 ,
,即
 .
.从而,梯形APQB的面积为
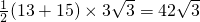 .
.分析:(1)由已知中正△ABC的边长为15,
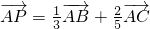 ,
,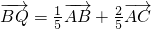 .根据向量加法的三角形法则,我们可得
.根据向量加法的三角形法则,我们可得 =
=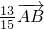 ,根据数乘向量的几何意义,我们可得
,根据数乘向量的几何意义,我们可得 ∥
∥ ,但|
,但| |≠|
|≠| |,进而根据梯形的判定定理得到四边形APQB为梯形;
|,进而根据梯形的判定定理得到四边形APQB为梯形;(2)根据已知条件,结合(1)中的结论,我们可得|
 |=13,|
|=13,| |=15,梯形APQB的高h为正△ABC的AB边上高的
|=15,梯形APQB的高h为正△ABC的AB边上高的 ,代入梯形面积公式,即可求出梯形APQB的面积.
,代入梯形面积公式,即可求出梯形APQB的面积.点评:本题考查的知识点是平面向量加法的三角形法则,数乘向量的几何意义,梯形面积公式,其中(1)的关键是根据向量加法的三角形法则,求出
 =
=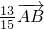 ,进而根据数乘向量的几何意义,分析PQ边与AB的关系,(2)的关键是根据已知求出梯形的上、下底边长及高的长度.
,进而根据数乘向量的几何意义,分析PQ边与AB的关系,(2)的关键是根据已知求出梯形的上、下底边长及高的长度. 
练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
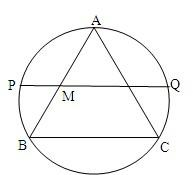 (选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
(选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
 如图,正△ABC的边长为15,
如图,正△ABC的边长为15,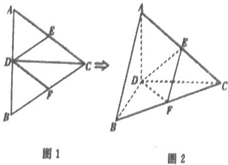 如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.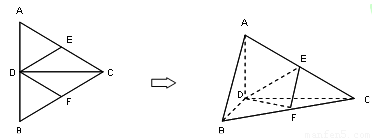
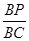 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.