题目内容
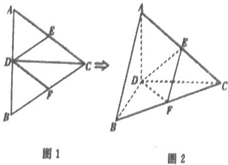 如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求异面直线AB与DE所成角的大小.
分析:(I)以D点为原点建立空间直角坐标系,利用向量的共线向量定理,证明线线平行,再由线线平行证线面平行;
(II)用坐标表示向量
和
,再利用向量的坐标运算求角的余弦值即可.
(II)用坐标表示向量
| EF |
| ED |
解答: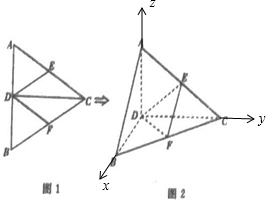 解:(I)如图2,建立空间直角坐标系,则
解:(I)如图2,建立空间直角坐标系,则
D(0,0,0),A(0,0,a),B(a,0,0),C(0,
a,0),E(0,
a,
),F(
,
a,0)
∴
=(a,0,-a),∴
=(
,0,-
),
∵
=
,
∴
∥
,∴AB∥EF,且EF?平面DEF,AB?平面DEF,
∴AB∥平面DEF
(II)∵AB∥EF,∴∠DEF即为异面直线AB与DE所成的角,
∴
=(0,
a,-
),
=(
,0,-
),
∴cos(
,
)=
=
=
.
∴异面直线AB与DE所成的角的大小为arccos
.
 解:(I)如图2,建立空间直角坐标系,则
解:(I)如图2,建立空间直角坐标系,则D(0,0,0),A(0,0,a),B(a,0,0),C(0,
| 3 |
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
∴
| AB |
| EF |
| a |
| 2 |
| a |
| 2 |
∵
| EF |
| 1 |
| 2 |
| AB |
∴
| EF |
| AB |
∴AB∥平面DEF
(II)∵AB∥EF,∴∠DEF即为异面直线AB与DE所成的角,
∴
| ED |
| ||
| 2 |
| a |
| 2 |
| EF |
| a |
| 2 |
| a |
| 2 |
∴cos(
| EF |
| ED |
| ||||
|
|
| ||||
a•
|
| ||
| 4 |
∴异面直线AB与DE所成的角的大小为arccos
| ||
| 4 |
点评:本题考查利用向量坐标运算为工具证明线线平行,求异面直线所成的角.关键是建立空间直角坐标系,正确的给出向量的坐标表示.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
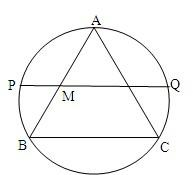 (选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
(选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
 如图,正△ABC的边长为15,
如图,正△ABC的边长为15,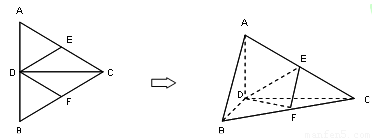
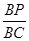 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.